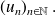Numeric sequences
Définition :
A numeric sequence is an application from
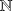(or a part of
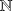) with values in
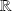or
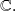
We write
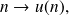or
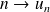, and we denote the sequence (meaning the application) by
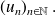
The numeric sequence
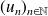is convergent if there exists
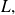belonging to
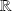or
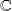such that:
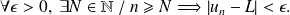
A non convergent sequence is said to be divergent.
We call
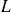the limit of the sequence and we denote it by:
Infinite limits
Let
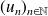be a real sequence:
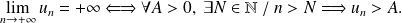
The definition is similar for a limit equal to
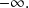
A sequence which goes to infinity is divergent. Convergent infers in
or
.
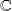Fondamental : Main sequence properties
The limit of a sequence, if it exists, is unique.
Every convergent sequence is bounded.
The set of numeric sequences can be provided with a vector space structure and an inner product.
The sum or the product of two convergent sequences is a convergent sequence, which has as a limit the sum or the product of the original limits.
If a sequence has a non zero finte limit, there exists an index beyond whihch the sequence is never zero. We can then define an inverse sequence, which is convergent and has as a limit the inverse of the original limit. We have the same result for a quotient of sequences, and expand it in special cases to zero or infinite limits, the cases where we cannot say anything being the indeterminated forms that are similar to the ones seen for applications.
Any real increasing sequence with an upper bound (or decreasing with a lower bound) is convergent.
Définition : Subsequences
Let
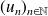be a numeric sequence and
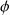be a strictly increasing application from
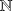to
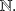
We call subsequence of sequence
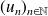the sequence
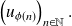
Exemple :
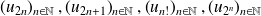are subsequences of sequence
