Take 5 minutes to prepare this exercise.
Then, if you lack ideas to begin, look at the given clue and start searching for the solution.
A detailed solution is then proposed to you.
If you have more questions, feel to ask then on the forum.
Question
For any natural integer
 greater or equal to
greater or equal to
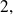 we define the application
we define the application
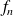 from
from
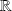 to
to
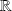 by:
by:

Prove that equation
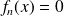 has a unique solution in interval
has a unique solution in interval
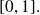
Study the variations of function
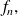 then the sign of its values in
then the sign of its values in
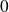 and in
and in
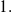
Use then the bijection's theorem.
Application
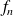 is differentiable, hence continuous, by the generic theorems.Let us sutdy the variations of application
is differentiable, hence continuous, by the generic theorems.Let us sutdy the variations of application
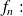

hence
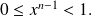
This implies that application
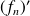 is strictly negative on interval
is strictly negative on interval
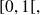 therefore that application
therefore that application
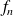 is strictly decreasing on
is strictly decreasing on
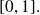
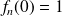 and
and
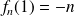 hence application
hence application
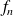 defines a bijection from
defines a bijection from
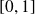 to
to
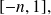 which implies that it takes once and only once the zero value.
which implies that it takes once and only once the zero value.





