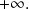Take 10 minutes to prepare this exercise.
Then, if you lack ideas to begin, look at the given clue and start searching for the solution.
A detailed solution is then proposed to you.
If you have more questions, feel to ask then on the forum.
Question
Find the following limits:
a)
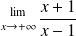
b)
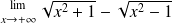
c)
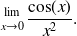
a) Divide the numerator and the denominator by
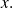
b) Multiply the numerator and the denominator by
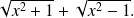
c) Apply the calculation rules on the limits, this is not an indeterminated form.
a) We have an indeterminated form
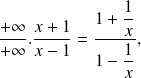 we know that
we know that
 converges towards
converges towards
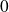 when
when
 goes to
goes to
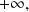 it is a limit to know, hence
it is a limit to know, hence
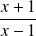 goes towards
goes towards
 when
when
 goes to
goes to
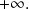
We can also use a more generic result: the limit of a quotient of two polynomials is equal to the limit of the quotient of the terms of higher degree.
b) We have an indeterminated form
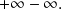
We multiply it by the “conjugated expression” :
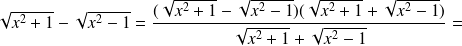
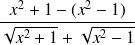
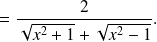
The denominator is the sum of two functions going to
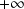 when
when
 goes to
goes to
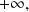 hence it goes to
hence it goes to
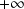 and the inverse goes towards
and the inverse goes towards
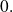
c) When
 goes towards
goes towards
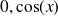 goes towards
goes towards
 and
and
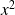 goes towards
goes towards
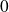 by positive values, hence the quotient goes to
by positive values, hence the quotient goes to