Take 10 minutes to prepare this exercise.
Then, if you lack ideas to begin, look at the given clue and start searching for the solution.
A detailed solution is then proposed to you.
If you have more questions, feel to ask then on the forum.
Question
We denote by
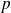and
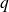two real numbers and by
a natural integer greater or equal to
.
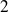Prove that equation
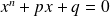has at most two roots if
is even and at most three if
is odd.
Differentiate application
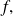study, depending on the parity of the natural integer
the number of zeros of the derivative application, then apply Rolle's theorem.
We set
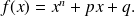
Application
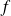is differentiable and has for derivative
Let us assume that
is even,
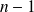is odd and equation
which is equivalent to
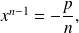has exactly one solution, since application
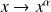is bijective from
to
when
is an odd integer.
Let us assume that application
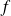is zero in three distinct points,
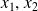and
From Rolle's theorem, application
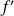is at lest once zero in intervals
and
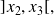hence in two distinct points, which in impossible. We infer that application
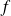can take the zero value at most twice.
If
is odd,
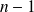is even and equation
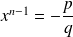has at most two roots, since if equation
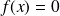had four roots, application
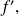still with Rolle's theorem, would be at least zero once at least between each root, which would mean three solutions for equation f'(x)=0, which is contradictory and we conclude that equation
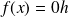as at most three solutions.
