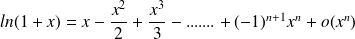Taylor-expansion
Définition :
Let
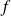be an application from
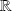to
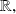a Taylor-expansion of
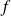around
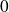is an approximation of application
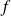by a polynomial with an upper bound of the error.
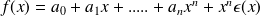with
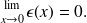
We also denote
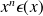by
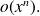
We say that
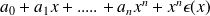is the Taylor-expansion of
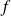of order
around
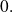
The Taylor-expansion of order
of an application around
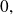when it exists, is unique.
We also define a Taylor-expansion around a real
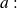
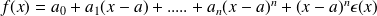with
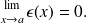
We also denote
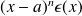by
and we have the same definitions and properties as for the Taylor-expansion around
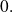
Taylor-Youg's formula
Let
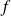be an application of class
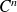around a point
. We have:
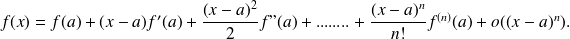
By setting
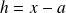we obtain another expression which is often useful:
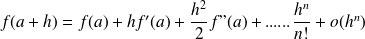
This infers that an application of class
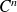around
has a Taylor-expansion of order
Taylor-Young's formula allows to determine the usual Taylor-expansions around
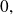that are useful to know, and it is used to determine a Taylor-expansion around a point
which differs from
Fondamental : Operations on Taylor-expansions
Sum
If two applications
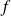and
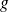have Taylor-expansions of order
around a real number
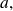application
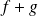has a Taylor-expansion of order
around
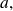equal to the sum of the Taylor-expansions of
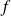and
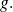
Product
If two applications
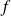and
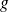have Taylor-expansions of order
around a real number
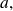of type
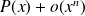and
) where
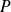and
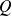are polynomials, the product
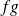has a Taylor-expansiion of order
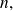equal to the part with a degree lower or equal to
of polynomial
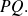
Integration
If application
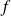has around
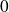a Taylor-expansion of order
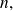of type
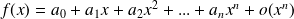and if we denote by
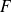the antiderivative which is zero in
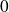of application
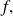we have:
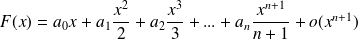
Fondamental : Taylor-expansions of usual applications around 0
Exponential application and associated applications
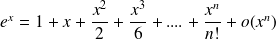
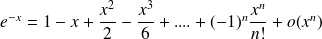
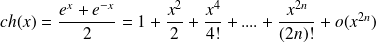(expansion of order
)
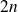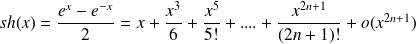(expansion of order
)
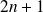Trigonométric applications
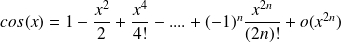(expansion of order
)
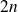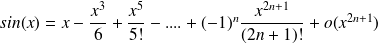(expansion of order
)
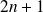Application
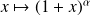
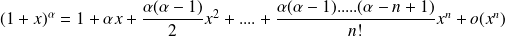
Special case
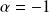and associated applications
With the expression of the sum of the terms of a geometric sequence, we have:
By changing
to
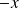we obtain:
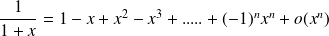
By integration we obtain:
