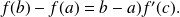Differentiable applications
Définition : Differentiable applications
Let
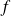 be an application defined on an open interval
be an application defined on an open interval
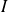 of
of
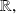 with values in
with values in
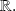
Let
 and
and
 be two elements of
be two elements of
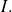
We call growth rate of
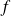 between
between
 and
and
 the quotient
the quotient
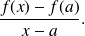
We say that application
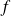 is differentiable in
is differentiable in
 if the growth rate has a finite limit when
if the growth rate has a finite limit when
 goes towards
goes towards
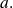
The real number
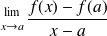 is called derivative number of application
is called derivative number of application
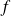 in
in
 and denoted by
and denoted by
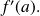
If the growth rate has a rigth-sided limit when
 goes to
goes to
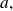 we say that application
we say that application
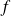 is differentiable from the rigth in
is differentiable from the rigth in
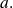
We define similarly the applications that are differentiable from the left.
Geometric interpretation
The derivative number
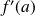 of a differentiable application in point
of a differentiable application in point
 is the slope of the tangent line of the graphical representation of application
is the slope of the tangent line of the graphical representation of application
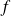 in the point of coordinates
in the point of coordinates
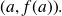
Derivative application
If an application
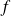 is differentiable in any point of an interval
is differentiable in any point of an interval
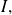 we define an application from
we define an application from
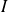 to
to
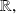 denoted by
denoted by
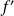 and called derivative application of application
and called derivative application of application
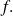
Fondamental : Sum, produic, quotient and composite of differentiable applications
Let
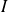 be an interval of
be an interval of
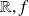 and
and
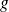 two differentiable applications on
two differentiable applications on
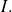
Application
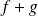 is differentiable and
is differentiable and
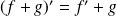 '
'
Application
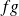 is differentiable and
is differentiable and
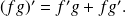
If application
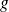 does not take the zero value on interval
does not take the zero value on interval
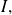 application
application
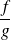 is differentiable and
is differentiable and
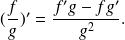
Let
 and
and
 be two intervals of
be two intervals of
 a differentiable application from
a differentiable application from
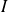 to
to
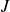 and
and
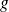 an application from
an application from
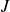 to
to
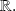
Application
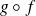 is differentiable on
is differentiable on
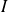 and
and
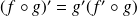
Differentiability of the inverse of a bijective application
Let
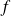 be a bijective differentiable application defined on an interval
be a bijective differentiable application defined on an interval
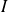 of
of
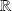 and with values in an interval
and with values in an interval
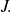
Application
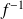 is differentiable in a point
is differentiable in a point
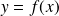 belonging to
belonging to
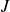 if and only if
if and only if
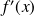 is non zero and we have:
is non zero and we have:
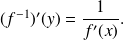
The derivative application of application
 is
is
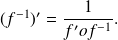
Fondamental : Derivative and direction of variation of an application
Let
 be a differentiable application on an interval
be a differentiable application on an interval
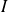 of
of
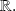
If application
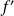 is positive on interval
is positive on interval
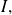 application
application
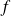 is increasing on
is increasing on
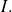
If application
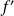 is negative on interval
is negative on interval
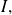 application
application
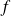 is decreasing on
is decreasing on
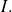
Définition : Derivatives of upper orders
Let
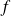 be a differentiable application on a interval
be a differentiable application on a interval
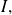 with values in
with values in
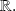
If application
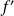 is continuous on
is continuous on
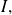 we say that application
we say that application
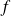 is of class
is of class
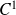 on
on
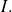
If application
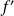 is differentiable, we denote by
is differentiable, we denote by
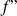 its derivative, called second derivative of function
its derivative, called second derivative of function
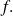
If the second derivative of
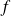 is continuous, we say that
is continuous, we say that
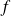 is of class
is of class
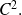
We can define in a recursive way the derivative of order
 of
of
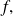 which will be called of class
which will be called of class
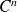 if it has a continuous derivative of order
if it has a continuous derivative of order
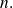
If function
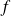 is of class
is of class
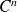 for any natural integer
for any natural integer
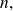 we say it is of class
we say it is of class
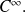
Fondamental : Rolle's theorem, formula of mean value
Rolle's theorem
Let
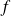 be a continuous application on a segment
be a continuous application on a segment
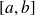 of
of
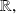 differentiable on
differentiable on
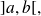 such that
such that
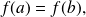 then:
then:
There exists a point
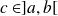 such that
such that
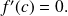
Formula of mean value
Let
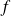 be a continuous application on
be a continuous application on
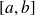 and differentiable on
and differentiable on
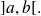
There exists
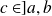 [ such that
[ such that