Continuous applications
Définition :
Let
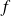be an application defined on an open interval
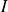of
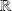and with values in
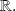
We say that application
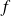is continuous in
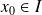if:
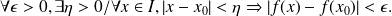
We say that application
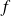is continuous on interval
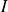if it is continuous in any point of interval
Exemple :
The polynomial, sinus, cosinus and exponential applications are continuous on
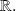
An algebraeic fraction, meaning an application of type
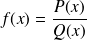where
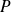and
are polynomials is continuous in any real number
such that
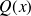is non zero.
The logarithm application is continuous on
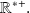
Fondamental : Operations on continuous applications
Sum, product, quotient
Let
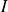be an open interval of
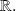
We denote by
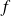and
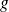two continuous applications on
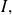then:
Applications
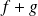and
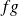are continuous on
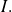
Application
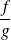is continuous in any point
such that
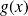is non zero.
Composite of two continuous applications
Let
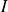and
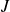be two open intervals of
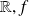a continuous application from
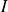to
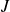and
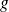a continuous application from
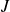to
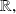then:
Application
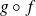is continuous on
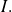
Inverse of a continuous application
Let
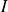and
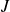be two intervals of
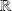and
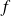an bijective application from
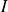to
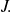
The inverse application of
denoted by
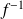is continuous from
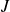to
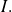
Fondamental : Properties of continuous applications
Intermediate value theorem
Let
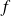be a continuous application on an open interval
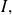
and
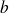two elements of
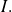
We have:
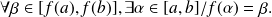
This means that if application
takes two values, it takes at leat once every value between these two values.
Theorem of bijection
Let
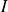be an interval of
and
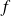a continuous and strictly monotonous application from
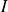to
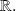
Then the image
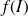of application
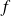is an interval of
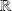and application
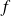defines a bijection from
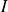to
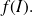
The graph representation of application
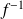is the symetrix of the graph representation of
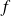with respect to the first bissecting line (meaning the line of equation
Continuous application on a segment
Let
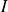be an open interval of
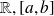a segment included in
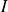and
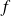a continuous application from
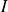to
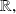then:
Application
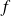is bounded on
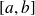and it reaches its bounds.
