Take 15 minutes to prepare this exercise.
Then, if you lack ideas to begin, look at the given clue and start searching for the solution.
A detailed solution is then proposed to you.
If you have more questions, feel to ask then on the forum.
Question
We denote by
 a strictly positive real number and by
a strictly positive real number and by
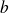 a real number belonging to interval
a real number belonging to interval
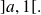
We define two real sequences
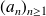 and
and
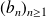 by:
by:
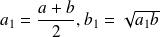 and for any integer
and for any integer
 greater or equal to
greater or equal to

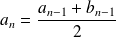 and
and
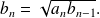
Find the limits of sequences
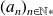 and
and
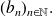
We can set
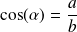 and look for the expressions of the sequences depending on
and look for the expressions of the sequences depending on
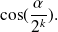
Express
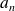 and
and
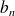 in the form of a product of
in the form of a product of
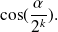
To find the limit of
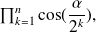 write it as quotient of
write it as quotient of
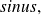 starting from
starting from
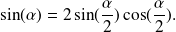
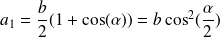
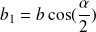
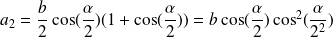
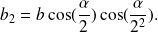
Let us assume:
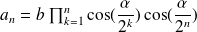
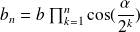
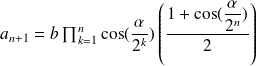
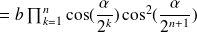
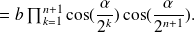
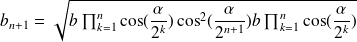
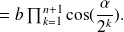
The expressions of
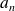 and
and
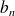 are therefore justified by recursion for any natural integer
are therefore justified by recursion for any natural integer
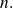
There remains to calculate the limit when
 goes to infinity of
goes to infinity of
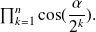

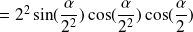
We obtain recursively:

We infer:
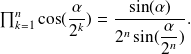
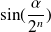 is equivalent to
is equivalent to
 when
when
 goes to infinity, therefore:
goes to infinity, therefore:
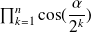 goes towards
goes towards
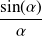 when
when
 goes to infinity. This implies that both sequences converge towards
goes to infinity. This implies that both sequences converge towards
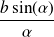 .
.





