Take 15 minutes to prepare this exercise.
Then, if you lack ideas to begin, look at the given clue and start searching for the solution.
A detailed solution is then proposed to you.
If you have more questions, feel to ask then on the forum.
Question
We denote by
 an interval of
an interval of
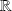 and by
and by
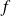 and
and
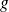 two applications defined from
two applications defined from
 to
to
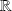 that are continuous in a point
that are continuous in a point

a) Prove that application
 is continuous in
is continuous in
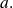
b) Prove that if application
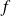 is continuous in a point
is continuous in a point
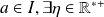 such that application
such that application
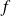 is bounded on
is bounded on

c) Prove that application
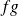 is continuous in
is continuous in
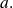
a) Write the definition of the continuity of both applications in
 with
with
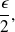 then use the triangular inequality.
then use the triangular inequality.
b) Write the definition of the continuity in
 with
with
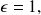 then use the triangular inequality with the form
then use the triangular inequality with the form
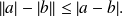
c) Start from:

then use the triangular inequality then the previous question.
a) Let
 be a strictly positive real number.
be a strictly positive real number.
Functions
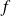 and
and
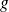 being continuous in
being continuous in
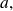 there exist two strictly positive real numbers
there exist two strictly positive real numbers
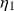 and
and
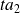 such that:
such that:


We then set
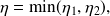 and using the triangular inequality, we obtain:
and using the triangular inequality, we obtain:

This reasonning can be made for any strictly positive real number
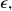 hence we proved that function
hence we proved that function
 is continuous in
is continuous in
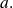
b) We set
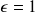 and write the definition of continuity in
and write the definition of continuity in
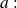
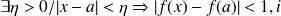

 being an open interval and
being an open interval and
 we can choose
we can choose
 small enough such that
small enough such that
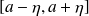 in included in
in included in

We then use the triangular inequality :
 which implies:
which implies:
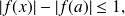 meaning:
meaning:
 therefore application
therefore application
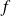 is bounded on
is bounded on

c) With the triangular inequality, we obtain:
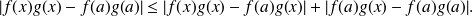
We consider an interval
 included in
included in

Application
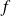 is bounded on interval
is bounded on interval
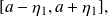 hence there exists a real number
hence there exists a real number
 which we can assume is non zero, such that:
which we can assume is non zero, such that:


Similarly, there exists a real non zero number
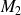 such that:
such that:
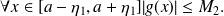
We then set

Let
 be a strictly positive real number.
be a strictly positive real number.
Functions
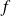 and
and
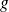 being continuous in
being continuous in
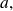 there exists two real numbers
there exists two real numbers
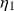 and
and
 such that:
such that:

We also have:

We then set
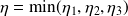 and we obtain:
and we obtain:
 .
.
The strictly positive real number
 being arbitrary, this infers that function
being arbitrary, this infers that function
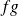 is continuous in
is continuous in