Finite limits
Définition :
Let
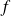 be an application defined on an open interval
be an application defined on an open interval
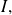 except in one point
except in one point
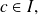 with values in
with values in
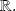
We say that application
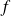 admits as limit
admits as limit
 when
when
 goes towards
goes towards
 if application
if application
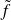 defined on
defined on
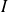 by:
by:
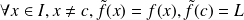 is continuous in
is continuous in
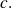
Application
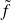 is called prolongation by continuity of application
is called prolongation by continuity of application
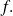
We denote this by
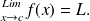
Equivalent definition:
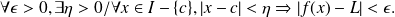
One-sided limits
We denote by
 and
and
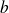 two real numbers,
two real numbers,
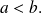
Let
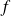 be an application defined on interval
be an application defined on interval
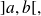 with values in
with values in
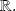
We say that application
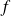 admits
admits
 as left-sided limit when
as left-sided limit when
 goes to
goes to
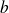 if:
if:
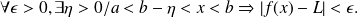
We then write
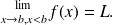
We say that application
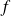 admits
admits
 as right-sided limit when
as right-sided limit when
 goes to
goes to
 if:
if:
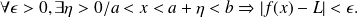
We then write
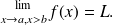
Fondamental : Relation between one-sided limits and limit, one-sided continuity
Let
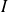 be an open interval of
be an open interval of
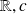 an element of
an element of
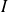 and
and
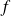 an application from
an application from
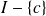 to
to
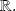
Application
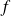 has a limit when
has a limit when
 goes towards
goes towards
 if and only if
if and only if
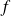 has a right-sided limit and a left-sided limit when
has a right-sided limit and a left-sided limit when
 goes towards
goes towards
 and these limits are equal.
and these limits are equal.
We then have :
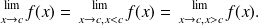
Let
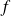 be a function defined on an interval
be a function defined on an interval
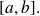
We define a function
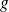 on
on
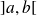 by
by
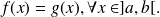
We say that function
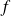 is continuous from the left in
is continuous from the left in
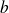 if
if
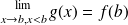
and continuous from the right in
 if
if
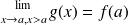
We define in a similar way the continuity from the left and from the right in one point
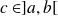 and function
and function
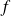 is continuous in
is continuous in
 if and only if it is continuous from the right and from the left in
if and only if it is continuous from the right and from the left in
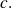
Fondamental : Operations on limits, sum, product, quotient, composition
Let
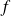 and
and
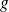 be two applications defined on an open interval
be two applications defined on an open interval
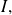 except in one point
except in one point
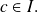
We assume :
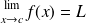 and
and
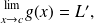 then:
then:
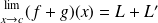
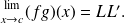
If we assume that
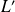 is non zero
is non zero
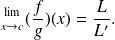
We denote by
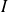 and
and
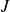 two intervals from
two intervals from
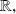 by
by
 an element of
an element of
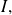 by
by
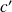 an element of
an element of
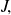 by
by
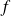 an application defined from
an application defined from
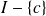 to
to
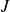 and by
and by
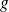 an application defined from
an application defined from
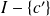 to
to
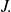
We assume:
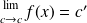 and
and
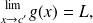 then:
then:
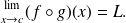
We have the same results for one-sided limits.





