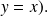Take 15 minutes to prepare this exercise.
Then, if you lack ideas to begin, look at the given clue and start searching for the solution.
A detailed solution is then proposed to you.
If you have more questions, feel to ask then on the forum.
Question
a) Prove that application
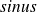defines a bijection between intervals
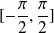and
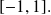
Draw the graphical representations of both applications.
The inverse application is denoted by
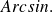
b) Find two intervals
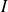and
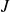such that application
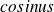defines a bijection from
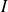to
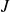and draw the graphical representations.
a) and b) Use the bijection's theorem. Reminder: The graphical representation of the inverse application of a bijective application
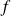is the symmetrical curve of the graphical representation of
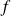with respect to the first bisector.
a) Application
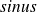has for derivative application the application
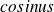which is strictly positive on interval
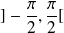hence function
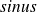is stricly increasing from
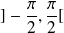to ]
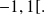
It is also continuous (it is a reference function) hence it is bijective from
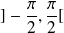to
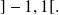
The graphical representation of the inverse application can be obtained from the one of application
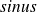by symmetry with respect to the first bissector (meaning the line of equation
).
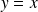b) The derivative application of application
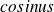is application
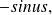which is strictly negative on interval
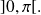
Application
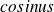is therefore strictly decreasing from
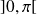to ]
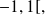it is also continuous (it is a reference function) hence it defines a bijection between these two intervals.
The graphical representation of the inverse application can be obtained from the one of application
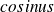by a symmetry with respect to the first bissector (meaning the line of equation
