Vector spaces of finite dimension
Définition :
A vector space is a finite dimension if it admits a finite generating familly.
All the bases of a vector space of finite dimension are finite and have the same number of elements.
This natural integer is called the dimension of vector space
By convention, the vector subspace
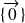has a dimension
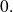
is a
-vector space of dimension
is a
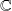-vector space of dimension
and a
-vector space of dimension
Fondamental : Specific properties of vector spaces of finite dimension
1. In a vector space of dimension
any linearly independent familly has at most
elements, any generating familly has at least
elements.
2. The bases of a vector space of finite dimension are the maximal linarly independent famillies and the minimal generating famillies.
3. In a vector space of dimension
every linearly independent familly of
elements is a basis, every generating familly of
elements is a basis.
Fondamental : Theorem of the incomplete basis
Let
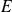be a vector space of finite dimension,
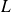a linearly independent familly of vectors of
a generating familly of vectors of
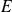such that
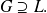
Then there exists a basis
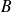of
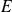such that:
This theorem is frequently used in a weaker form:
Let
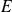be a vector space of finite dimension.
Every linearly independent familly
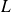of vectors of
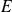can be completed in a basis of
Définition : Coordinates of a vector in a basis
Let
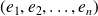be a basis of a vector space
Every vector
of
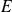can be written in a unique way as a linear combination of vectors of
Meaning:
such that:
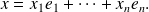
The element of
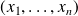is called the system of coordinates of
in basis
To ensure the unicity it is imperative that the order of the vectorrs in the basis is fixed, it important to pay attention to that point when using the "canonical basis" of vector space of matrices.
Fondamental : Change of basis formulas
Let
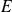be a vector space of dimension
and
are two bases of
We call matrix of change of basis
to basis
the matrix whose columns are the coordinates of vectors
in basis
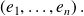
More precisely, if we denote by
the change of basis matrix, with
we have
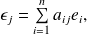for any
between
and
We denote by
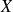and
the matrices (with one column and
rows) of coordinates of a vector
of
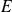in basis
and in basis
we then have
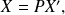meaning:
We can notice that this formula has no practical interest since we generally change from basis
to basis
so we know
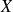and look for
However a change of basis matrix is invertible and we infer the formula
which gives what we are looking for depending on what we know. We “only” need to calculate
