Take 10 minutes to prepare this exercise.
Then, if you lack ideas to begin, look at the given clue and start searching for the solution.
A detailed solution is then proposed to you.
If you have more questions, feel to ask then on the forum.
Question
The polynomial
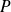is of degree
of leading coefficient
and admits
distinct complex roots,
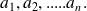
We denote by
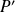the derivative polynomial of
Prove that for any complex number
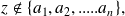we have:
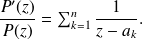
Indice
Use the Gauss's factorization of the polynomial :
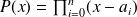then express polynomial
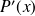as a product.
Solution
By the factorization theorem of Gauss, we have:
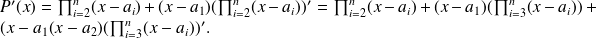
Iterring the calculation, we get:
This results in:
