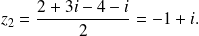Take 15 minutes to prepare this exercise.
Then, if you lack ideas to begin, look at the given clue and start searching for the solution.
A detailed solution is then proposed to you.
If you have more questions, feel to ask then on the forum.
Question
Solve the following second degree equations in
1.
2.
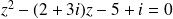
In both cases, calculate the discriminant
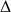then by setting
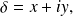determine
such that
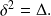
You can use the relation
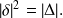
a) The discriminant of the second degree equation
is equal to
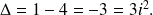
The solutions of the second degree equation are:
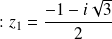et
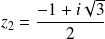
b) The discriminant of the second degree equation
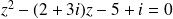is equal to:
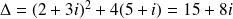
We look for a complex number
such that
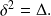
Real numbers
and
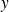must satisfy:
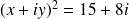which is equivalent to:
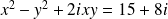which gives us, identifying real and imaginary parts:
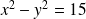(1)
(2)
We must also have
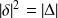which gives:
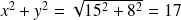(3)
Summing equations (1) and (3), we obtain:
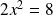
Substracting equations (3) and (1), we obtain :
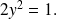
From equation (2), real numbers
and
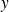have the same sign, hence the solutions for complex number
are:
or
We infer the solutions of the second degree equation:
