Roots of a polynomial
Définition :
Let
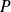be an element of
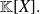
An element
of
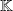is a root of polynomial
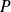if
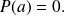
Fondamental : Gauss' factorization
If
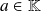is a root of
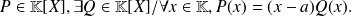
Fondamental : Multiplicity order of a root
Let
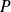be an element of
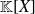and
a root of polynomial
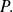
From the previous theorem, there exists a polynomial
such that
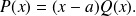
If
is not a root of
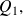meaning if
we say that
is a simple root (or of order
) of
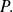
If
is a root of polynomial
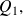by appliying Gauss' theorem, there exists a polynomial
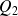such that
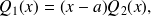which gives us:
If
is not a root of polynomial
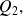we say that
is a double root, or of order
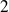of polynomial
If
is a root of polynomial
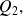we go on.
We build this way a sequence of polynomials
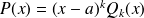with strictly decreasing degrees, hence we end up with:
with
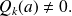
We then say that
is a root of order
of polynomial
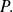
Theorem
Let
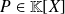and
be an element of
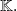
is a root of order
of polynomial
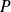if and only if
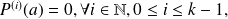where
denotes the derivative of order
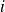of polynomial
with the convention
