Take 10 minutes to prepare this exercise.
Then, if you lack ideas to begin, look at the given clue and start searching for the solution.
A detailed solution is then proposed to you.
If you have more questions, feel to ask then on the forum.
Question
Determine a sufficient and necessary condition on real numbers
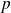and
and on natural integer
such that equation
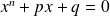admits a double real root.
If there is a double root, it is also a root of polynomial
Determine
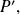the hypothetic roots of polynomial
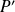must be roots of polynomial
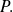
If the polynomial
defined by
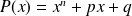has a double root
is a root of the polynomial and of the derivative polynomial
Real number
must therefore satisfy:
andn
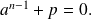
We infer from the second equation :
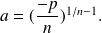
Replacing this in the first equation, we obtain:
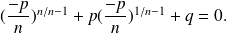
Conversely, if equality
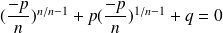is satisfied, the complex numbers
such that
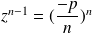are roots of the equation and its derivative equation, hence are double root of the equation. If one of these numbers is real, the equation has a real double root.
The second condition is always satisfied if
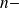is odd, hence if
is even.
