Linear combinations, linearly independant famillies, generating famillies, bases, dimension
Définition : Linear combinations
Let
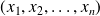 be a familly of
be a familly of
 vectors of a
vectors of a
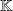 -vector space
-vector space
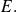
We call linear combination of these vectors any vector of type
 belonging to
belonging to
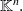
The scalars
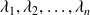 are called the coefficients of the linear combination.
are called the coefficients of the linear combination.
Définition : Linearly independent famillies
A familly
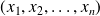 of vectors of a vector space
of vectors of a vector space
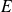 is linearly independent if the only linear combination of these vectors equal to the zero vector is the one whose coefficients are all zero.
is linearly independent if the only linear combination of these vectors equal to the zero vector is the one whose coefficients are all zero.
We also say that vectors
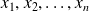 are linearly independent.
are linearly independent.
This can be expressed as:
 is a linearly independent familly) is equivalent to:
is a linearly independent familly) is equivalent to:

Définition : Linearly dependent famillies
A non linearly independent familly is called a linearly dependent familly.
We also say that vectors
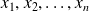 are linearly dependents.
are linearly dependents.
This can be expressed as:
 is a linearly dependent familly is equivalent to
is a linearly dependent familly is equivalent to
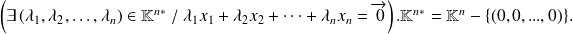
Définition : Generating famillies
A familly
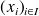 is generating a vector space
is generating a vector space
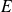 if any vector of
if any vector of
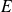 is equal to a linear combination of vectors of the familly, meaning:
is equal to a linear combination of vectors of the familly, meaning:

Définition : Bases
A basis of a vector space is linearly independent generating familly.





