Ring of polynomials
Définition :
We denote by
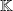a field egal to
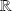or
We call polynomial with coefficients in
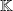a finite sequence
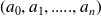of elements of
The set of polynomials with coefficients in
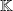is denoted by
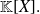
To any polynomial
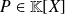is associated a polynomial application with coefficients in
defined by:
Remarque :
We often confue the polynomial with the polynomial application which it defines on
A polynomial
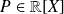defines a polynomial application from
to
and a polynomial application from
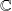to
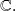
Définition :
We call degree of polynomial
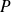the natural integer
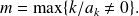
Remarque :
Writing
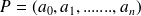does not mean that polynomial
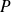is of degree
it may be of degree
in which case
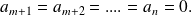
Définition : Addition and multiplication
Let
and
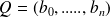be two polynomials with coefficients in
The sum of polynomials
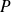and
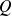is polynomial:
The product of polynomials
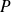and
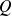is the following polynomial:
Remarque :
This definition can be surprizing, it is better understood when considering the product of the associated polynomial applications:
Fondamental : Properties of the addition of polynomials
The addition of polynomials is commutative :
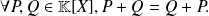
The addition of polynomials is associative :
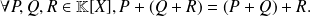
There exists a neutral element for the addition of polynomials, the zero polynomial,
which satisfies:
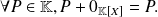
For any polynomial
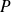there exists a symmetric element for the addition.
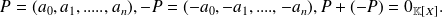
Fondamental : Proprerties of the product of polynomials
The product of polynomials is commutative:
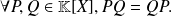
The product of polynomials is associative:
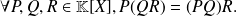
There exists a neutral element for the product of polynomials, the constant polynomial equal to
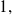noted
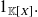
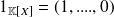which satisfies:
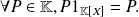
The product of polynomials is distributive with respect to the addition:
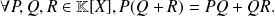
We summarize all these properties by saying that the tuple constituted of
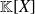and both laws of addition and multiplication is a commutative ring.
