Take 10 minutes to prepare this exercise.
Then, if you lack ideas to begin, look at the given clue and start searching for the solution.
A detailed solution is then proposed to you.
If you have more questions, feel to ask then on the forum.
Question
Prove that the familly of vectors of
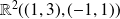is a generating familly of vectors of
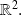
Prove that for any pair
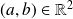the system of equations which is equivalent to the equality
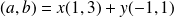has one solution.
Let
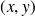be an element of
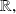we look for two real numbers
and
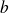such that:
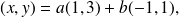which is equivalent to:
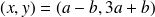which results in the system:
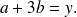
We obtain by calculating the difference between both equations:
then, using the first equation :
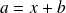
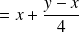
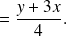
We proved that every element
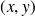of
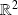can be written as a linear combination of
and
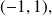therefore the family is a generating set of
