The field of complex numbers
Définition :
Definition of two laws of internal composition on
We define on set
two internal composition laws:
• an addition:
• a multiplication:
Algebraic notation:
We notice that
and by denoting by
the element
and by
the element
we have:
By applying the definition of multiplication, we have:
with the previous identification, which is coherent with the usal calculation:
and we find the definition of the multiplication.
Fondamental : Properties
• the addition is associative :
• there exists a neutral element for the addition :
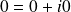
• for any element
of
there exists a symmetric element for the addition:
• the addition is commutative:
• the multiplication is associative:
• there exists a neutral element for the multiplication:
• For any non zero element of
there exists a symmetric element for the multiplication:
• the multiplication is commutative:
• the multiplication is distributive with respect to the addition:
Définition :
The tuple constituted of set
and both laws of internal composition is a field, called field of complex numbers and denoted
The element
of
considered as an element of
and denoted
this notation being called algebraic form of the complex number
The real number
is called real part of the complex number
and denoted by
the real number
is called est imaginary part of
denoted by
Fondamental : Properties
Equality of two complex numbers:
Two complex numbers are equal if and only if their real parts and their imaginary parts are respectively equal.
