Force s'exerçant sur un tuyau d'évacuation
(20 minutes de préparation)
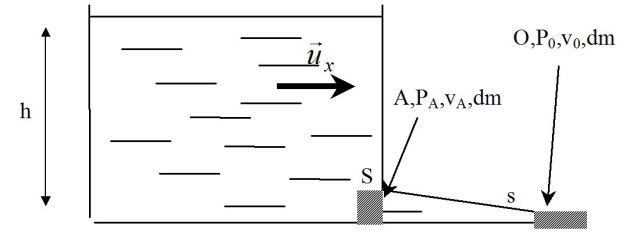
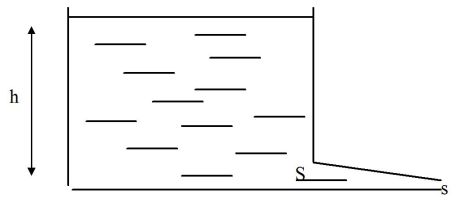
A la base de la paroi verticale d'un récipient rempli de liquide sur une hauteur h est percé un petit orifice de section S sur lequel est emmanché un tuyau horizontal conique dont l'autre extrémité a une section \(s=\alpha S\) (avec \(\alpha<1\)).
En précisant les hypothèses adoptées :
Question
Calculer la pression P au niveau de la section S. Examiner les cas limites \(\alpha=0\) et \(\alpha=1\).
Indice
Utiliser le théorème de Bernoulli et la conservation du débit pour déterminer les grandeurs inconnues
Faire un bilan de quantité de mouvement sur un système fermé
Solution
On fait l'hypothèse d'un régime quasi-stationnaire (h varie lentement).
Le théorème de Bernoulli donne alors en A et en B :
\(P_0 + \mu gh = P_A + \frac{1}{2}\mu v_A^2 = P_0 + \frac{1}{2}\mu v_0^2\)
Ainsi :
\(v_0 = \sqrt {2gh} \;\;\;\;\;\;\;\;et\;\;\;\;\;\;\;\;P_A = P_0 + \frac{1}{2}\mu (v_0^2 - v_A^2 )\)
La conservation du débit massique entre A et O donne :
\(Sv_A = sv_0 = \alpha Sv_0 \;\;\;\;\;\;\;\;\;\;soit\;\;\;\;\;\;\;\;\;\;v_A = \alpha v_0 = \alpha \sqrt {2gh}\)
D'où la pression en A :
\(P_A = P_0 + \mu gh(1 - \alpha ^2 )\)
Remarque :
Si \(\alpha=0\) : \(P_A=P_0+\mu gh\) (pression hydrostatique)
Si \(\alpha=1\) : \(P_A=P_0\) (pression uniforme dans le tube)
Question
Exprimer, en fonction de \(\alpha\), h et S la force F qui tend à arracher le tube.
Solution
On raisonne sur le système fermé suivant (voir figure):
Le contenu du tube et une masse dm qui va entrer à travers S entre les instants t et t + dt.
En régime quasi-stationnaire, la même masse dm va sortir à travers la section s pendant dt. On a bien sur :
\(dm = \mu v_A Sdt = \mu v_0 sdt\)
Ce système fermé est soumis aux forces extérieures :
Son poids, \(m\vec g\)
Les forces de pression à l'entrée et à la sortie, \(P_AS\vec u_x-P_0s\vec u_x\)
La force exercée par le tube sur l'eau, égale à l'opposée de la force exercée par l'eau sur le tube (qui est celle que l'on cherche) notée ainsi \(-\vec F\)
Le théorème de la résultante cinétique donne :
\(\frac{{D\vec p}}{{Dt}} = m\vec g + P_A S\;\vec u_x - P_0 s\;\vec u_x - \vec F\)
Or :
\(\frac{{D\vec p}}{{Dt}} = \frac{{dm}}{{dt}}(v_0 - v_A )\;\vec u_x = \mu v_A S(v_0 - v_A )\;\vec u_x = 2\mu ghS\;\alpha (1 - \alpha )\;\vec u_x\)
Et :
\(P_A S\;\vec u_x - P_0 s\;\vec u_x = \left[ {P_0 S + \mu gh(1 - \alpha ^2 )S - P_0 \alpha S} \right]\;\vec u_x = \left[ {P_0 + \mu gh(1 + \alpha )} \right]\;(1 - \alpha )S\;\vec u_x\)
D'où l'expression de la force :
\(\vec F = \left[ {P_0 + \mu gh(1 + \alpha )} \right]\;(1 - \alpha )S\;\vec u_x - 2\mu ghS\;\alpha (1 - \alpha )\;\vec u_x + m\vec g\)
Soit :
\(\vec F = P_0 (1 - \alpha )S\;\vec u_x + \mu ghS\;(1 - \alpha )^2 \;\vec u_x + m\vec g\)
On obtient une force qui a tendance à arracher le tube vers la droite.
Si \(\alpha =0\) : on retrouve encore les lois de l'hydrostatique.
Si \(\alpha =1\), la force est nulle.