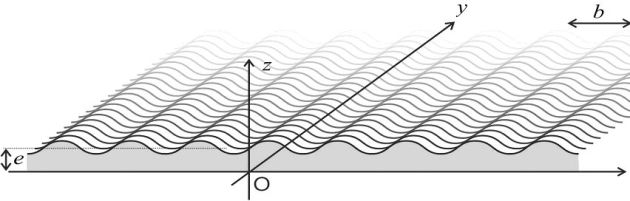
Film de peinture
(20 minutes de préparation)
On étudie l'évolution d'un film de peinture d'épaisseur e (selon Oz), après un coup de pinceau sur une surface horizontale, les poils laissant des stries distantes de b (selon Ox).
La peinture est assimilée à un fluide newtonien incompressible de viscosité \(\eta\) et de masse volumique \(\mu\) :
\(\eta = 0,12\;Pl\;;\;\mu = {1,2.10^3}\;kg.{m^{ - 3}}\;;\;e = 0,1\;mm\;;\;b = 1\;mm\)
Question
Justifier la forme de la vitesse :
\(\vec v = {v_x}(x,z,t){\vec u_x} + {v_z}(x,z,t){\vec u_z}\)
Montrer que \(v_x>>v_z\).
Dans la suite, la composante verticale de la vitesse est négligée. On propose une solution de la forme :
\(\vec v = {v_0}g(z)\sin \left( {\pi \frac{x}{b}} \right){e^{ - \frac{t}{\tau }}}{\vec u_x}\)
Les forces de pression et le poids sont négligés devant les forces de viscosité.
Solution
Il y a invariance selon Oy. Le fluide étant incompressible \(div \vec v=0\), soit :
\(\frac{{\partial {v_x}}}{{\partial x}} + \frac{{\partial {v_z}}}{{\partial z}} = 0\)
On effectue un calcul d'ordre de grandeur :
\(\frac{{\partial {v_x}}}{{\partial x}} \approx \frac{{{v_x}}}{b}\;\;\;\;\;;\;\;\;\;\;\frac{{\partial {v_z}}}{{\partial z}} \approx \frac{{{v_z}}}{e}\)
Comme \(e>>b\), \(v_x>>v_z\)
Question
Exprimer les conditions aux limites en z = 0 et z = e.
Solution
Les conditions aux limites sont :
\(v(0) = 0\;et\;\eta {\left( {\frac{{\partial v}}{{\partial z}}} \right)_{z = e}} = 0,\;soit\;g(0) = 0\;et\;g'(e) = 0\)
Question
Montrer que l'accélération convective est négligeable devant les autres termes de l'équation de Navier Stockes.
Solution
On effectue de nouveau un calcul d'ordre de grandeur :
\(\eta \Delta v = \eta \left( {\frac{{{\partial ^2}v}}{{\partial {x^2}}} + \frac{{{\partial ^2}v}}{{\partial {z^2}}}} \right) \approx \eta \left( {\frac{v}{{{b^2}}} + \frac{v}{{{e^2}}}} \right) = \eta \frac{v}{{{e^2}}}\;;\;\frac{{\mu \left\| {\vec v.\overrightarrow {grad} v} \right\|}}{{\eta \Delta v}} \approx \frac{{\mu \frac{{{v^2}}}{b}}}{{\eta \frac{v}{{{e^2}}}}} = \frac{{\mu v{e^2}}}{{\eta b}} < < 1\)
Question
Déterminer l'équation différentielle vérifiée par g(z). Déterminer \(\tau\), commenter.
Solution
L'équation de Navier – Stockes devient simplement :
\(\mu \frac{{\partial v}}{{\partial t}} = \eta \frac{{{\partial ^2}v}}{{\partial {x^2}}} + \eta \frac{{{\partial ^2}v}}{{\partial {z^2}}}\;\;\;\;\;soit \;\;\;\;\;g''(z) + \left( {\frac{\mu }{{\eta \tau }} - \frac{{{\pi ^2}}}{{{b^2}}}} \right)g(z) = 0\)
La solution est de la forme :
\(g(z) = A\cos \frac{z}{\delta } + B\sin \frac{z}{\delta }\;\;\;\;\;\;\;\left( {\frac{1}{{{\delta ^2}}} = \frac{\mu }{{\eta \tau }} - \frac{{{\pi ^2}}}{{{b^2}}}} \right)\)
Comme \(g(0)=0\), \(A=0\).
La condition \(g'(e)=0\) conduit à :
\(cos(e/\delta)=0\)
Soit :
\(\frac{e}{\delta } = (2p + 1)\frac{\pi }{2}\)
Ce qui permet de connaître la valeur de \(\tau\).