Le phénomène de Caléfaction (Leidenfrost effect)
(15 minutes de préparation)
Une goutte d'eau est en lévitation au-dessus d'une plaque chauffante de température \(T_p\).
La lévitation est due à la vaporisation de l'eau sous la goutte (voir la vidéo proposée ci-dessous).
On note \(a(t)\) le rayon de la goutte supposée hémisphérique et \(e(t)\) la distance entre la plaque et la face inférieure de la goutte.
Typiquement, le rayon initial de la goutte est \(a_0=1\;mm\) et la durée \(\tau\) d'existence de la goutte est de l'ordre de la minute.
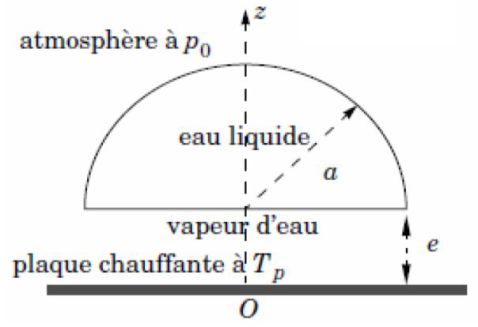
L'interprétation qualitative de la caléfaction a été proposée par Leidenfrost en 1756 : la plaque, de température plus élevée que celle de la goutte, cède à celle-ci de la chaleur, ce qui provoque l'évaporation progressive de la goutte liquide.
Cette évaporation, qui n'est pas isotrope, provoque un écoulement de vapeur d'eau sous la goutte qui permet à celle-ci de léviter au-dessus de la plaque.
Question
Déterminer l'équation vérifiée par la température \(T(r,z,t)\) de la vapeur d'eau située entre la plaque et la face inférieure de la goutte.
On note \(D_{th}\) le coefficient de diffusivité thermique de la vapeur d'eau.
On donne le laplacien en coordonnées cylindriques :
\(\Delta f = \frac{1}{r}\frac{\partial }{{\partial r}}\left( {r\frac{{\partial f}}{{\partial r}}} \right) + \frac{1}{{{r^2}}}\frac{{{\partial ^2}f}}{{\partial {\theta ^2}}} + \frac{{{\partial ^2}f}}{{\partial {z^2}}}\)
Question
Donner une condition sur \(a\) et \(e\) pour que les dérivées partielles par rapport à \(r\) soient négligeables devant celles par rapport à \(z\).
On se place dans la suite dans cette hypothèse.
Question
Donner une relation entre \(e\), \(D_{th}\) et \(\tau\) pour que l'on puisse se placer en régime "quasi-stationnaire".
Question
Expliciter la solution \(T(r,z,t)\). La goutte liquide est à la température d'ébullition, notée \(T_e\), en \(z=e(t)\).
Question
On note \(\mu_{\ell}\) la masse volumique de l'eau liquide et \(\ell_v\) la chaleur latente massique de vaporisation de l'eau.
Montrer que \(a(t)\) vérifie l'équation différentielle :
\(\frac{{da}}{{dt}} = - \frac{\lambda }{{2e{\mu _\ell }{\ell _v}}}({T_p} - {T_e})\)
où \(\lambda\) est la conductivité thermique de la vapeur d'eau.
