Gel d'un lac
(15 minutes de préparation)
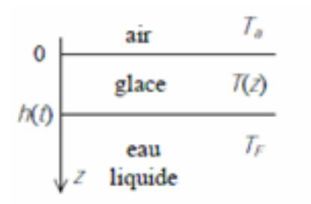
La température de l'air est Ta = 263 K et celle de l'eau liquide TF = 273 K.
On donne la chaleur latente de fusion de la glace Lf, sa masse volumique ρ et sa conductivité thermique λ.
La capacité thermique massique de la glace est supposée négligeable.
Question
Établir des équations différentielles vérifiées par T(z) et h(t).
Les résoudre et déterminer h(t).
Solution
L'équation de la chaleur dans la glace :
\(\rho c\frac{{\partial T}}{{\partial t}} = \lambda \frac{{{\partial ^2}T}}{{\partial {z^2}}}\)
Donne si on suppose que c est pratiquement nulle :
\(\frac{{{\partial ^2}T}}{{\partial {z^2}}} \approx 0\)
Soit :
\(T(z,t) = {T_a} + \frac{{{T_F}-{T_a}}}{{h(t)}}z\)
On se place dans le cadre de l'approximation des régimes quasi – stationnaires.
Le flux thermique dans la glace est dû à la solidification de la glace, soit, entre t et t + dt :
\(j(z,t) = - \lambda \frac{{\partial T}}{{\partial z}} = - \frac{{\lambda ({T_F}-{T_a})}}{{h(t)}}\)
D'où :
\(- \frac{{\lambda ({T_F}-{T_a})}}{{h(t)}}Sdt = - {L_F}dm = - \rho Sdh{L_F}\)
Soit :
\(\frac{{\lambda ({T_F}-{T_a})}}{{h(t)}}Sdt = \rho Sdh{L_F}\)
Et :
\(hdh = \frac{{\lambda ({T_F}-{T_a})}}{{\rho {L_F}}}dt\)
Par intégration :
\(h = \sqrt {\frac{{2\lambda ({T_F}-{T_a})}}{{\rho {L_F}}}\;t}\)