Quadripôle électrostatique
Consacrer 10 minutes de préparation à cet exercice.
Puis, si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Si vous avez des questions complémentaires, n'hésitez pas à les poser sur le forum.
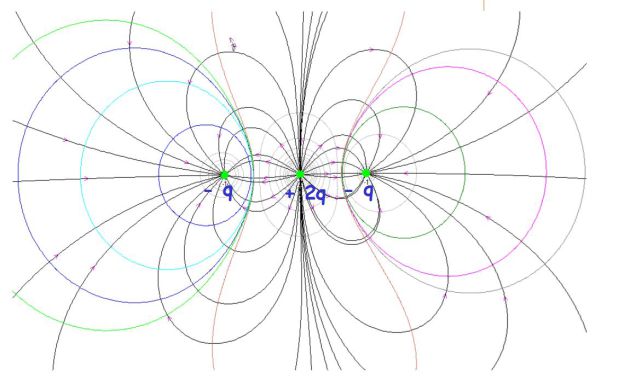
Soit un ensemble de trois charges alignées :
2 q en O, - q en A(+ a,0) et - q en B(- a,0).
Question
Calculer le potentiel puis le champ en un point M de l'espace situé à la distance r de O, en supposant r >> a.
Indice
La méthode est semblable à celle utilisée pour le dipôle électrostatique, mais le développement limité doit être fait au second ordre.
Solution
La méthode utilisée est similaire à celle utilisée pour le dipôle électrostatique.
On pose \(x=a/r\) et on utilise le développement limité de :
\({\left( {1 + x} \right)^{ - 1/2}} \approx 1 - \frac{1}{2}x\; + \frac{3}{8}{x^2}\)
Le potentiel créé en un point M est :
\(V(M) = \frac{q}{{4\pi {\varepsilon _0}}}\left( {\frac{2}{r} - \frac{1}{{AM}} - \frac{1}{{BM}}} \right)\)
Avec :
\(\frac{1}{{AM}} = \frac{1}{r}{\left( {1 - \frac{a}{r}\cos \theta + \frac{{{a^2}}}{{{r^2}}}} \right)^{ - 1/2}}\)
Et :
\(\frac{1}{{BM}} = \frac{1}{r}{\left( {1 + \frac{a}{r}\cos \theta + \frac{{{a^2}}}{{{r^2}}}} \right)^{ - 1/2}}\)
Un développement au 2nd ordre en \(a/r\) conduit à :
\(V(M) = \frac{q}{{4\pi {\varepsilon _0}}}\frac{{{a^2}}}{{{r^3}}}(1 - 3{\cos ^2}\theta )\)

Le champ électrostatique se calcule à partir de :
\(\left\{ \begin{array}{l}{E_r}(r,\theta ) = - \frac{{\partial V}}{{\partial r}} \\{E_\theta }(r,\theta ) = - \frac{1}{r}\frac{{\partial V}}{{\partial \theta }} \\\end{array} \right.\)
La figure suivante donne la topographie du champ (lignes de champs et lignes équipotentielles) :