Enroulement du vent autour d'un anticyclone et d'une dépression
(15 minutes de préparation)
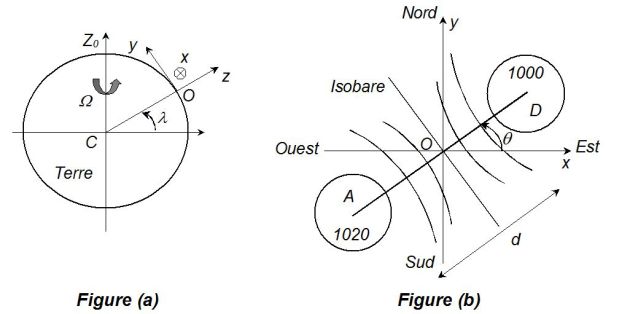
Un point M situé dans l'atmosphère terrestre est repéré par ses coordonnées (x,y,z) dans le repère local (Oxyz), dont l'origine O se trouve dans un plan méridien à la latitude λ, avec \(0 \le \lambda \le \pi /2\) pour l'hémisphère Nord (figure (a)).
L'axe (Ox) est dirigé vers l'Est, l'axe (Oy) vers le Nord et l'axe (Oz) suivant le rayon terrestre.
La vitesse angulaire de rotation propre de la Terre est \(\Omega = 2\pi /86\;164\;rad.{s^{ - 1}}\).
On considère la situation météorologique schématisée sur la figure (b), dans laquelle l'axe anticyclone-dépression fait un angle \(\theta\) avec la direction (Ox).
La distance entre les isobares PA = 1 020 et PD = 1 000 est notée d, les pressions étant mesurées en hectopascals.
On supposera le gradient de pression uniforme sur l'axe (AD), de norme notée a.
Au niveau de l'axe (AD), les isobares sont perpendiculaires à cet axe et sont localement assimilables à des segments de droite.
Question
Le référentiel géocentrique étant supposé galiléen, on se place dans le référentiel terrestre.
Écrire, en négligeant les forces de frottements, le principe fondamental de la dynamique pour la particule de fluide (de masse dm) dans le référentiel terrestre.
Solution
Le principe fondamental de la dynamique, écrit dans le référentiel terrestre non galiléen ne fait intervenir explicitement que la seule force d'inertie de Coriolis égale à \(- 2\,(dm)\,\vec \Omega \wedge \vec v\) (où \(\vec v\) désigne le vecteur vitesse de la particule de fluide de masse dm), puisque la force d'inertie d'entraînement est comprise dans la définition du poids .
Par conséquent, en négligeant les forces de frottement :
\((dm)\,\frac{{d\vec v}}{{dt}} = (dm)\,\vec g - 2\,(dm)\,\vec \Omega \wedge \vec v - \frac{{dm}}{\rho }\mathop {grad}\limits^ \to P\)
Soit :
\(\frac{{d\vec v}}{{dt}} = \vec g - 2\,\,\vec \Omega \wedge \vec v - \frac{1}{\rho }\mathop {grad}\limits^ \to P\)
Question
Exprimer les coordonnées \(f_x\) et \(f_y\) de la force massique de pression, le long de l'axe (AD), en fonction de a, \(\rho\) et \(\theta\).
Solution
Le long de l'axe (AD), le gradient de pression est uniforme et vaut, en norme :
\(a = ({P_A} - {P_D})/d\)
Vectoriellement, on en déduit en notant \(\vec u_r\) le vecteur unitaire de l'axe (AD) orienté de A vers D :
\(\mathop {grad}\limits^ \to P = - a\,{\vec u_r} = - a\,\cos \theta \,{\vec u_x} - a\,\sin \theta \,{\vec u_y}\)
D'où les expressions des coordonnées \(f_x\) et \(f_y\) de la force massique de pression :
\({f_x} = \frac{a}{\rho }\,\,\cos \theta\;\;\;\;et\;\;\;\;{f_y} = \frac{a}{\rho }\,\,\sin \theta\)
Question
L'approximation géostrophique consiste à négliger l'accélération du mouvement.
Montrer que le fluide atmosphérique s'écoule au niveau de l'axe (AD) suivant une direction et un sens que l'on précisera.
Comment modifier ces conclusions dans l'hémisphère Sud ?
Calculer la norme notée \(v\) du vecteur vitesse du vent. On donne :
\(d=800\;km\;\;\;\;\lambda=42°\;\;\;\;\rho=1,3\;kg.m^{-3}\)
Solution
Dans le cadre de l'approximation géostrophique, l'accélération \(d\vec v /dt=\vec 0\) et l'équation différentielle du mouvement devient alors : \(2\,\,\vec \Omega \wedge \vec v = \vec g - \frac{1}{\rho }\mathop {grad}\limits^ \to P\)
Avec :
\(\vec \Omega=\Omega(cos\lambda\;\vec u_y+sin\lambda\;\vec u_z)\) et \(\vec v = {v_x}\,{\vec u_x} + {v_y}\,{\vec u_y}\), on en déduit, en projection sur les axes (Ox) et (Oy) :
\(- 2\,\Omega \,{v_y}\sin \lambda = {f_x}\;\;\;\;et\;\;\;\;2\,\Omega \,{v_x}\sin \lambda = {f_y}\)
Les coordonnées de la vitesse de la particule, le long de l'axe (AD) sont ainsi :
\(\,\,{v_x} = \frac{{a\sin \theta }}{{2\rho \Omega \sin \lambda }}\;\;\;\;et\;\;\;\;\,\,{v_y} = -\frac{{a\cos \theta }}{{2\rho \Omega \sin \lambda }}\)
Le vecteur vitesse de la particule peut encore s'écrire sous forme vectorielle :
\(\,\,\vec v = \frac{a}{{2\rho \Omega \sin \lambda }}\left( {\sin \theta \,{{\vec u}_x} - \cos \theta \,{{\vec u}_y}} \right) = - \frac{a}{{2\rho \Omega \sin \lambda }}\,{\vec u_\theta }\)
où \(\vec u_{\theta} \) désigne le vecteur unitaire directement perpendiculaire au vecteur \(\vec u_r\) (figure ci-dessous).
Dans l'hémisphère Nord, pour lequel la latitude \(\lambda>0\), le vecteur vitesse est parallèle aux isobares et orienté dans le sens contraire au vecteur \(\vec u_{\theta}\).
Dans l'hémisphère Sud, pour lequel \(\lambda<0\), le vecteur vitesse est désormais de même sens que \(\vec u_{\theta} \).
Dans l'hémisphère Nord, le vent associé à une dépression souffle dans le sens inverse des aiguilles d'une montre et s'engouffre vers le centre dépressionnaire, alors que, pour un anticyclone, le vent sort du centre anticyclonique cette fois dans le sens des aiguilles d'une montre (voir figure de droite, ci-dessous).
Ces conclusions permettent d'expliquer la règle de Buys-Ballot (météorologiste hollandais, 1817-1890) déterminant la direction du centre d'une dépression d'après l'observation du vent : dans l'hémisphère Nord, le vent laisse les basses pressions à sa gauche (sur la droite dans l'hémisphère Sud) et plus les isobares sont serrées, plus le vent est fort .
Numériquement, avec :
\(a = ({P_A} - {P_d})/d = {2,5.10^{ - 3}}Pa.{m^{ - 1}}\)
la norme de la vitesse du vent le long de l'axe (AD) vaut :
\(v = 19,7\,m.{s^{ - 1}} = 71\,km.{h^{ - 1}}\)
Complément : Justification de l'approximation géostrophique
On va chercher un critère pour pouvoir négliger tous les termes contenant la vitesse dans l'équation d'Euler sauf celui dû aux forces de Coriolis.
Pour cela on se donne une vitesse caractéristique \(v\), une échelle spatiale caractéristique \(L\) et une durée caractéristique d'évolution \(\tau\) pour le champ des vitesses de telle sorte que :
\(\frac{{\left\| {\mu (\vec v.\overrightarrow {grad} )\vec v} \right\|}}{{\left\| {\mu \vec \Omega \wedge \vec v} \right\|}} \approx \frac{{\mu v(v/L)}}{{\mu \Omega v}} \approx \frac{v}{{L\Omega }}\)
Et :
\(\frac{{\left\| {\mu \frac{{\partial v}}{{\partial t}}} \right\|}}{{\left\| {\mu \vec \Omega \wedge \vec v} \right\|}} \approx \frac{{\mu (v/\tau )}}{{\mu \Omega v}} \approx \frac{1}{{\tau \Omega }}\)
Ainsi, pour des vents tels que \(v \approx 0,1\;m.s^{ - 1}\) évoluant sur une durée \(\tau\) supérieure à dix jours et sur des échelles spatiales de l'ordre d'au moins cinquante kilomètres, on a, avec \(\Omega = 7.10^{ - 5} \;rad.s^{ - 1} :\)
\(\frac{{\left\| {\mu (\vec v.\overrightarrow {grad} )\vec v} \right\|}}{{\left\| {\mu \vec \Omega \wedge \vec v} \right\|}} < 3.10^{ - 2} \;\;\;\;\;et\;\;\;\;\;\frac{{\left\| {\mu \frac{{\partial v}}{{\partial t}}} \right\|}}{{\left\| {\mu \vec \Omega \wedge \vec v} \right\|}} < 10^{ - 1}\)
Ceci permet de négliger l'accélération et d'écrire l'équation d'Euler sous la forme simplifiée :
\(- \overrightarrow {grad} P + \mu \vec g - 2\mu \vec \Omega \wedge \vec v = \vec 0\)