Oscillateurs couplés
Consacrer 15 minutes de préparation à cet exercice.
Puis, si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Si vous avez des questions complémentaires, n'hésitez pas à les poser sur le forum.
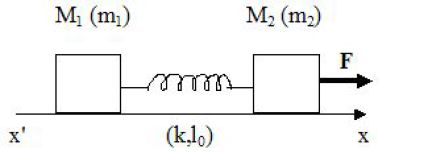
Deux masses m1 et m2 sont reliées par un ressort de raideur k et de longueur à vide \(\ell _0\).
Elles peuvent se déplacer sans frottement sur un axe horizontal (x'x).
Pour t < 0, le ressort est non tendu et les masses m1 et m2 sont au repos en M10 et M20.
A partir de t = 0, on exerce sur m2 une force horizontale constante \(\vec F = F\ \vec u_x\).
On note x1(t) = M10M1 et x2(t) = M20M2.
Question
Déterminer x1(t) et x2(t).
Indice
Appliquer le PFD à chacun des corps.
Solution
On applique le PFD à chacune des deux masses, en projection selon l'axe (Ox) :
\(m_1 \ddot x_1=k(\ell_0 +x_2 -x_1 - \ell_0)=k(x_2 -x_1 )\)
\(m_2 \ddot x_2=-k(x_2 -x_1 )+F\)
En faisant la somme des deux équations :
\(m_1\ddot x_1 + m_2 \ddot x_2 = F\)
Par intégration et tenant compte des CI :
\(m_1 x_1+m_2 x_2=\frac{1}{2} F t^2\)
On peut écrire les deux équations différentielles sous la forme :
\(\ddot x_1=\frac {k}{m_1}k(x_2 -x_1 )\)
Et :
\(\ddot x_2=-\frac {k}{m_2}(x_2 -x_1 )+\frac{F}{m_2}\)
En retranchant membre à membre ces deux équations :
\(\ddot x_2-\ddot x_1=-k(\frac {1}{m_1}+\frac{1}{m_2})(x_2 -x_1 )+\frac{F}{m_2}\)
On pose :
\(\Omega ^2= k(\frac {1}{m_1}+\frac{1}{m_2})\)
Alors :
\((\ddot x_2-\ddot x_1)+\Omega^2(x_2 -x_1 )=\frac{F}{m_2}\)
Dont la solution est :
\(x_2-x_1=Acos\Omega t + Bsin\Omega t + \frac{F}{m_2 \Omega^2}\)
Compte tenu des CI :
\(x_2-x_1=\frac{F}{m_2 \Omega^2}(1-cos\Omega t)\)
On peut ensuite en déduire \(x_1\) et \(x_2\) connaissant leur somme et leur différence.
Simulation : Animations JAVA de JJ.Rousseau (Université du Mans)
Deux oscillateurs harmoniques couplés : cliquer
Trois oscillateurs harmoniques couplés : cliquer
Oscillations d'une chaîne linéaire : cliquer
Oscillations d'une chaîne linéaire avec deux masses alternées : cliquer
Pendules élastiques superposés : cliquer