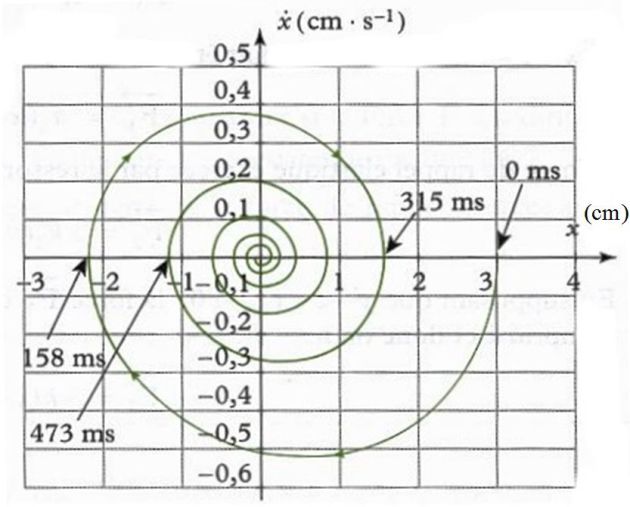
Phase portrait of an oscillator
Take 10 minutes to prepare this exercise.
Then, if you lack ideas to begin, look at the given clue and start searching for the solution.
A detailed solution is then proposed to you.
If you have more questions, feel free to ask them on the forum.
Let us consider the phase portrait of a damped harmonic oscillator : a mass \(m=500\;g\) having two forces exerted on : the elastic force of a spring (spring constant \(k\)), and a viscous fluid force (\(\vec f=-\lambda\vec v\)) , where \(\vec v\) is the velocity of the mass \(m\).
The mass is displayed of \(x\) with respect to its equilibrium position O.
The study is done in the inertial frame of reference of the laboratory.
Question
Find kind of oscillations are these ?
Solution
Underdamping : since there is friction, the phase curve is not closed.
It ends in an equilibrium point (here, O) called an attractive point.
Question
Graphically, find :
The initial position, \(x_0\).
The final position, \(x_f\).
The undamped period, \(T_a\).
The logarithmic decrement, \(\delta\).
Solution
By reading the diagram :
\(x_0=3\;cm\) and \(x_f=0\;cm\)
Also :
\(T_a=315\;ms\)
The logarithmic decrement is : (see the lesson "A few classical applications")
\(\delta = \ln \left( {\frac{{{x_0}}}{{{x_1}}}} \right) = \ln \left( {\frac{{{{3.10}^{ - 2}}}}{{{{1,6.10}^{ - 2}}}}} \right) = 0,628\;\;\;\;;\;\;\;\;x(t + {T_a}) = {e^{ - \delta }}x(t) = {e^{ - \sigma {\omega _0}{T_a}}}x(t)\)
Question
Deduce the undamped angular frequency \(\omega_0\), the \(Q\)-factor of the oscillator, the spring constant \(k\) and the viscous friction coefficient \(\lambda\).
Solution
We deduce :
\(Q=5\), \(\omega_0=20,05\;rad.s^{-1}\) and \(\sigma=1/2Q=0,1\)
Note that \(Q\) gives the order of magnitude of the number of visible oscillations.
Then :
\(k=m\omega_0^2=201\;N.m^{-1}\) and \(\lambda=m\frac{\omega_0}{Q}=2\;N.m^{-1}.s\)