Motions of charged particles inside electromagnetic fields
Fondamental : Electric field
Let us consider a punctual charged particle M (\(+q\)) of mass \(m\) in motion in a uniform electrostatic field \(\vec E_0\).
The frame of study is the one of the laboratory. It is supposed to be inertial.
The second law of motion gives the equation of the position of M :
\(m\frac{{d\vec v}}{{dt}} = q\vec E\;\;\;\;\;so\;\;\;\;\;\frac{{d\vec v}}{{dt}} = \frac{q}{m}\vec E\)
We can see an analogy with a material point placed in a uniform gravity field :
\(m\frac{{d\vec v}}{{dt}} = m\vec g\;\;\;\;\;so\;\;\;\;\;\frac{{d\vec v}}{{dt}} = \vec g\)
Thus the motion of the particle will either be a straight line or a parabola.
Fondamental : Magnetic field
Power of the magnetic force :
Let us consider a punctual charged particle M (\(+q\)) of mass \(m\) in motion in a uniform magnetostatic field \(\vec B_0\).
The frame of study is the one of the laboratory, it is supposed to be inertial.
The second law of motion gives the equation of the position of M :
\(m\frac{{d\vec v}}{{dt}} = q\vec v \wedge \vec B\)
The power of the magnetic force is zero (\(P = (q\vec v \wedge \vec B).\vec v = 0\)).
By using the work energy theorem :
\(P = \frac{{d{E_c}}}{{dt}} = 0\;\;\;\;\;so\;\;\;\;{E_c} = cste\;\;\;\;and\;\;\;\;\;v = cste\)
A magnetic field does not change the norm of the velocity vector : it only changes its direction.
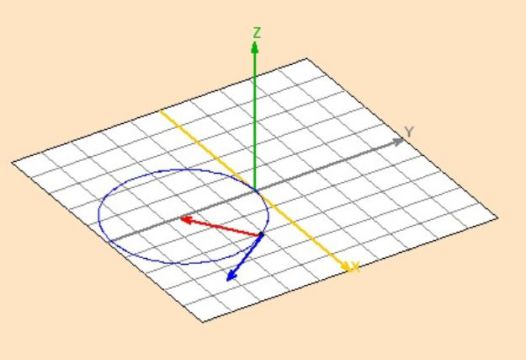
Circular motion :
Let us consider a punctual charged particle M (\(+q\)) of mass \(m\) in motion in a uniform magnetostatic field \(\vec B_0=B_0\vec u_z\).
The initial velocity of the particle is perpendicular to the field.
It is, for instance, along the (Ox) axis :
\(\vec v_0=v_0 \vec u_x\)
The second law of motion will give the radius of the circle (we suppose \(q>0\)) :
\(m\frac{v_0^2}{R}=qv_0B_0\)
So :
\(R=\frac{mv_0}{qB_0}\)
The particle moves in a circular orbit with a constant angular velocity (called cyclotron angular velocity) :
\(\omega_0=\frac{v_0}{R}=\frac{qB_0}{m}\)
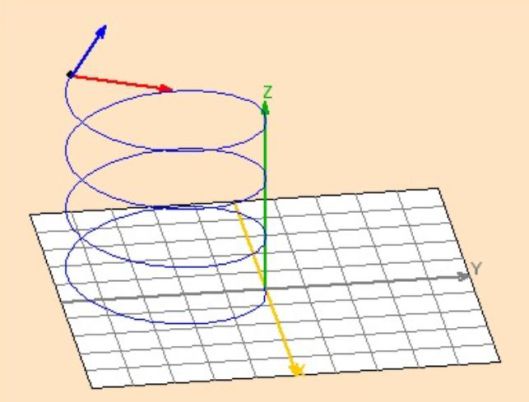
Helical motion :
Let us consider a punctual charged particle M (\(+q\)) of mass \(m\) in motion in a uniform magnetostatic field \(\vec B_0=B_0\vec u_z\).
The initial velocity of the particle is given. By picking the axises right, we write it :
\({\vec v_0} = {v_0 }\sin \alpha \;{\vec u_x}\; + \;{v_0 }\cos \alpha \;{\vec u_z}\)
The trajectory contained in the plane perpendicular to the (Oz) axis is a circle of radius :
\(R=\frac{mv_0sin\alpha}{qB}\)
which the particle follows with a constant angular velocity \(\omega_0\).
The trajectory with respect to the (Oz) axis is rectilinear and uniform.
The particle speed is : \(v_0cos\alpha\;\vec u_z\).
The trajectory is a helix with constant pitch.
This pitch \(h\) (the width the particle travels after one period of the circular motion) is :
\(h=\frac{2\pi}{\omega_0}v_0cos\alpha\)
Some videos about motions in magnetic field (http://physics-animations.com/) :
Fondamental : Electric and magnetic fields
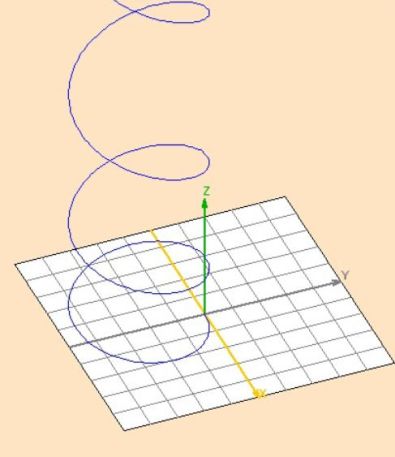
Helix with variable pitch :
Let us consider a punctual charged particle M (\(+q\)) of mass \(m\) in motion in a uniform magnetostatic field \(\vec B_0=B_0\vec u_z\) and a uniform elctrostatic field \(\vec E_0=E_0\vec u_z\).
The initial velocity of the particle is given. By picking the axises right, we write it :
\({\vec v_0} = {v_0 }\sin \alpha \;{\vec u_x}\; + \;{v_0 }\cos \alpha \;{\vec u_z}\)
With respect to the axis (Oz), the motion is accelerated :
\(z(t)=\frac{qE_0}{2m}t^2+v_0cos\alpha\)
Cycloid :
Let us consider a punctual charged particle M (\(+q\)) of mass \(m\) in motion in a uniform magnetostatic field \(\vec B_0=B_0\vec u_z\) and a uniform elctrostatic field \(\vec E_0=E_0\vec u_y\).
The particle is initially at the origin O. Its initial velocity is zero.
We note :
\({\omega _c} = qB/m\)
We can show that the parametric equations of the trajectory are :
\(x = \frac{E}{{B{\omega _c}}}({\omega _c}t - \sin {\omega _c}t)\;\;\;\;;\;\;\;\;y = \frac{E}{{B{\omega _c}}}(1 - \cos {\omega _c}t)\;\)
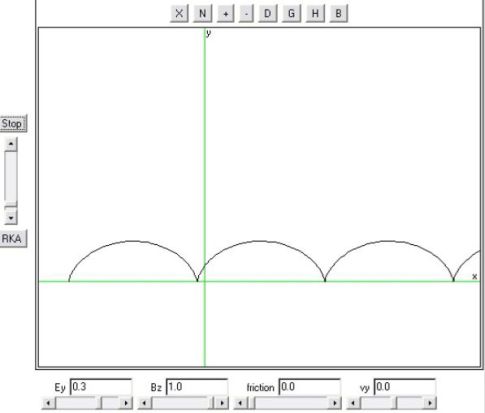
Une animation Java sur un filtre de vitesse et la mesure du rapport e / m :
Animation java (Jean-Jacques Rousseau, Université du Mans), cliquer ici :
Une vidéo illustrant le mouvement d'une particule dans des champs électrique et magnétique croisés (http://physics-animations.com/) :