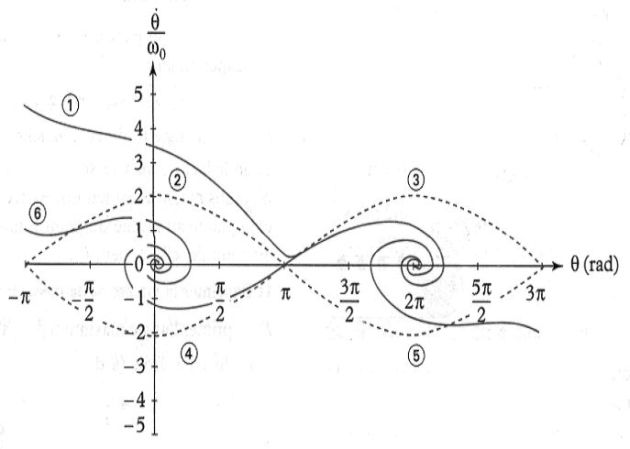
Phase portrait
Fondamental : Notion of state space
It is the product of the usual space by the velocity space.
In this space, a material point M is characterized by the coordinates of its position vector \((x,y,z)\) and of its velocity vector \((v_x,v_y,v_z)\).
We will only study the case where the motion of M is unidirectional, along the axis (Ox).
The equivalent of M in the state space is then moving along a two-dimensional plane.
The coordinates of this point are \((x,v)\). When M is in motion, it moves along a curve called « phase curve ».
The origin of the trajectory is the point M0\((x_0,v_0)\) : it is the initial state of M.
The position of the material point is completely determined by the initial values and by the knowledge of the motion equations.
Since the evolution of the particle is unique, two trajectories cannot intersect.
If it was possible, by taking this point for initial value, two distinct solutions of the motion equations could be found : it cannot be for mathematical reasons.
Exemple : Phase portrait
Let us consider a pendulum of length \(\ell \) which we display sideways with an angle\( \theta_0\).
Fluid friction are acting on it. The differential equation is :
\(\ddot \theta + h\;\dot \theta + \omega _0^2\;\sin \theta = 0\)
Its phase portrait is given, with :
\({\omega _0} = 5\;rad.{s^{ - 1}}\;\;and\;\;h = 0,5\;{s^{ - 1}}\)
How can we see that there are frictions ?
Place stable and unstable steady states.
Comment on the different curves.
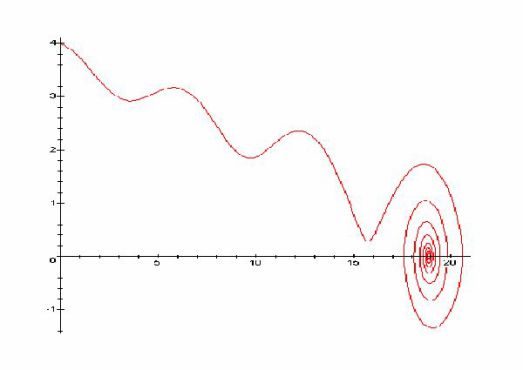
How can we interpret the curve found below ?