Launching conditions of a satellite
Take 15 minutes to prepare this exercise.
Then, if you lack ideas to begin, look at the given clue and start searching for the solution.
A detailed solution is then proposed to you.
If you have more questions, feel free to ask them on the forum.
A satellite is injected in orbit on M0. The distance between M0 and the center O of the Earth is \(r_0\).
Its initial velocity is \(\vec v_0\). it is orthogonal to \(\overrightarrow {OM} _0\).
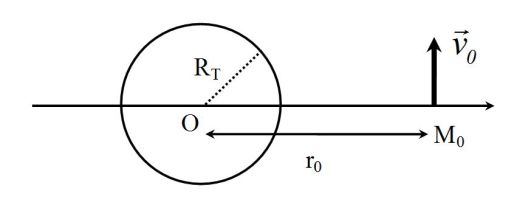
Question
Express this velocity \(\vec v_0\) with \(G\), \(M_T\) (mass of the Earth) and \(r_0\) if the trajectory is a circle of radius \(r_0\).
In the following questions, we note this particular velocity \(v_c\).
Solution
The second law of motion for a circular motion is :
\(m\frac{{v_c^2}}{{{r_0}}} = G\frac{{m{M_T}}}{{r_0^2}}\;\;\;\;\;so\;\;\;\;\;\;{v_c} = \sqrt {\frac{{G{M_T}}}{{{r_0}}}}\)
Question
If \(R_T\) is the radius of the Earth, we note :
\(\lambda = \frac{{r_0 }}{{R_T }}\)
Show that the satellite will not escape the gravitational pull of the Earth and will not meet the Earth if :
\(\frac{2}{{1 + \lambda }} < \left( {\frac{{v_0 }}{{v_c }}} \right)^2 < 2\)
Indice
What is the mechanical energy on a parabola ? On an ellipse ?
Solution
The satellite escapes the gravitational pull of the Earth if its mechanical energy cancels out (its motion is a parabola).
The velocity \(v_0\) is such as :
\({E_m} = \frac{1}{2}mv_0^2 - G\frac{{m{M_T}}}{{{r_0}}} = 0\;\;\;\;\;so\;\;\;\;\;{v_0} = \sqrt {2\frac{{G{M_T}}}{{{r_0}}}} = \sqrt 2 \;{v_c}\)
If the satellite touches the Earth, its trajectory is an ellipse with a major axis of length :
\(2a=r_0+R_T\)
The energy for an elliptical motion is :
\({E_m} = - \frac{{Gm{M_T}}}{{2a}} = - \frac{{Gm{M_T}}}{{{r_0} + {R_T}}}\)
This energy is equal to the one it had when it was launched :
\({E_m} = \frac{1}{2}mv_0^2 - G\frac{{m{M_T}}}{{{r_0}}} = - \frac{{Gm{M_T}}}{{{r_0} + {R_T}}}\)
We can deduce the corresponding value of \(v_0\) :
\(v_0^2 = 2G{M_T}\frac{{{R_T}}}{{{r_0}({r_0} + {R_T})}} = 2\frac{{G{M_T}}}{{{r_0}}}\frac{1}{{\lambda + 1}}=\frac{2}{1+\lambda}v_c^2\)
Finally, the satellite does not espace the Earth's gravitational pull and does not meet the Earth if :
\(\frac{2}{{1 + \lambda }} < {\left( {\frac{{{v_0}}}{{{v_c}}}} \right)^2} < 2\)