Slide
Take 10 minutes to prepare this exercise.
Then, if you lack ideas to begin, look at the given clue and start searching for the solution.
A detailed solution is then proposed to you.
If you have more questions, feel free to ask them on the forum.
A child, supposed to be a material point G of mass \(m = 40\) \(kg\), slides on a circular slide of radius \(r=2,5\) \(m\) from the position \(\theta (0)=\theta_0=15°\) where its velocity is zero until the position \(\theta_1=90°\) where he leaves the slide.
Forces of friction are neglected.
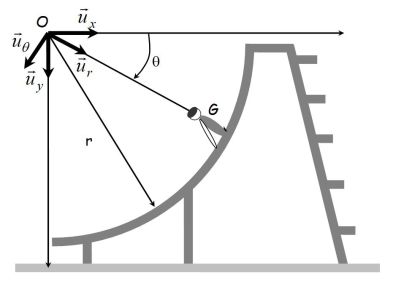
Question
By first using the second law of motion for moments of force, then the conservation of mechanical energy, find the equation of the motion of the child.
Solution
The second law is :
\(m{r^2}\ddot \theta {\;\vec u_z} = {\vec M_{poids/O}} = mgr\cos \theta {\;\vec u_z}\)
It follows :
\(\ddot \theta = \frac{g}{r}\cos \theta\)
Mechanical energy of the child :
\({E_m} = \frac{1}{2}m{r^2}{\dot \theta ^2} - mgr\sin \theta\)
It is conserved :
\(\frac{{d{E_m}}}{{dt}} = m{r^2}\dot \theta \ddot \theta - mgr\dot \theta \cos \theta\)
Thus :
\({r}\ddot \theta - g \cos \theta=0\)
These equations are the same.
Question
Find the velocity of the child as a function of \(\theta\).
Calculate the maximum speed of the child. Comment on this value.
Solution
By integrating the motion :
\({E_m} = \frac{1}{2}m{v^2} - mgr\sin \theta = -mgr\sin {\theta _0}\)
We deduce \(v\) :
\(v = \sqrt {2gr(\sin \theta - \sin {\theta _0})}\)
We can also multiply by \(\dot \theta\) and integrate the equation :
\(\ddot \theta = \frac{g}{r}\cos \theta\)
This is the same expression as \(v=r\dot \theta\).
This velocity is quite high : luckily, frictions help to reduce this speed and allow the child not to hurt himself.