Non-inertial frame of reference :
Fondamental : Weight definition
Weight is the resulting force of the gravitational force exerted by the Earth and of the centrifugal inertial force, due to the rotation of the Earth.
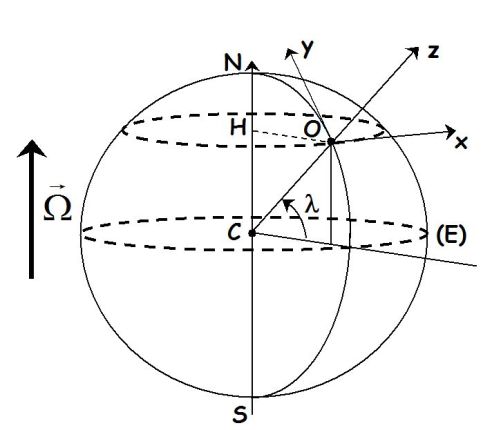
Let us assimilate the Earth to a sphere of center O, of radius \(R_T\) and of spherical mass repartition.
The weight of a mass \(m\) on the surface is :
\(mg = \frac{{G{m M_T}}}{{R_T^2}} - m\Omega _T^2{R_T}{\cos ^2}\lambda\)
\(M_T\) is the mass of the Earth, \(G\) the gravitational constant, \(\Omega_T\) the angular velocity of the rotation of the Earth relative to its North-South axis and \(\lambda\) the latitude of the point M where we write \(g\) (see figure).
The direction of \(\vec g\) gives the vertical axis of M.
Note :
On the figure, the centrifugal component is exaggerated for easier comprehension.
The term \(\Omega_T^2 R_T cos^2\lambda\) cannot be greater than :
\((\Omega_T^2 R_T cos^2\lambda)_{max}=\Omega_T^2 R_T =3,4.10^{-2}m.s^{-2}<<\frac{GM_T}{R_T^2}\approx 9,8\;m.s^{-2}\)
We note :
O : Paris
Ox : orientated towards the East, tangent to the latitude
Oy : orientated towards the North, tangent to the meridian
Oz : collinear to the radius CO, orientated towards space
\(\lambda\) is the latitude of M
\(\Omega\) is the angular velocity of the Earth relative to NS :
\(\vec \Omega = \Omega (\cos \lambda \;{\vec u_y} + \sin \lambda \;{\vec u_z})\;\;\;\;\;with\;\;\;\;\;\Omega \approx {7,3.10^{ - 5}}rad.{s^{ - 1}}\)
Note :
Because of its rotation, the Earth is not really spherical : it is a bit flatter on the poles.
Let us define the reference ellipsoid : the theoretical shape which is the closest to the real shape of the Earth.
It is defined by :
Its major axis : \(a=6\;378,160\;km\)
Its flattening, \(f\), defined by :
\(f=\frac{a-c}{c}=\frac{1}{298,257}\)
where \(c\) is the polar radius.
The value of \(c\) is about : \(c=6\;357\;km\), which is a \(21\) \(km\) difference between the polar radius and the equatorial radius (a relative difference of \(0,3\)%).
The mathematical shape which resembles the Earth the most is not a sphere, but it looks a lot like one !
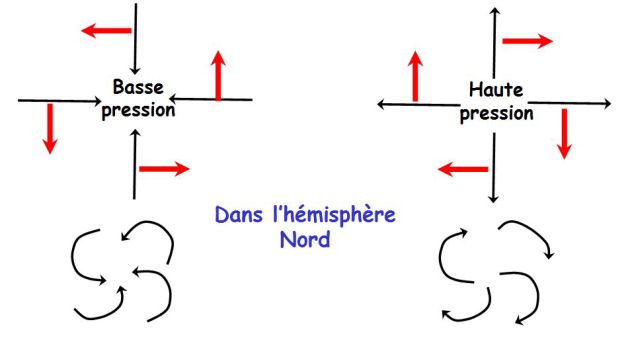
Exemple : Consequences of the Coriolis forces : depression circulation, anticyclone circulation
For motions that are parallel to the ground :
A material point is moving along a parallel or a meridian.
The Coriolis force is always orientated right of the motion (in the Northern hemisphere) and left of the motion (in the Southern hemisphere).
Let us demonstrate that with the definition of the Coriolis force :
\({\vec f_{ic}} = - \;2m\vec \Omega \wedge \vec v'\)
In the Northern hemisphere :
The right side of rivers is often more washed than the left one.
Railroads are more worn out on the right.
Circulation of depression and anticyclones :
The following figure explains succinctly the circulation of depression and anticyclones in the northern hemisphere (it is the opposite in the southern hemisphere).
Fondamental : Consequences of the Coriolis forces : east deviation
For a vertical free fall : (the notations are the one of the first figure)
A point is initially on the (Oz) axis at an altitude \(h\).
It is dropped without speed. (friction is neglected)
If we suppose the terrestrial reference frame to be inertial, the free fall is vertical and we write :
\({v_z} = - {g_0}t\;\;;\;\;z = - \frac{1}{2}{g_0}{t^2} + h\)
If we take into account the Coriolis force, there is an additional motion : (the force is along (Ox), with \(x>0\))
\({\vec f_{ie}} = - 2m\vec \Omega \wedge {v_z}{\vec u_z} = - 2m\Omega (\cos \lambda \;{\vec u_y} + \sin \lambda \;{\vec u_z}) \wedge {v_z}{\vec u_z}\)
It follows :
\({\vec f_{ie}} = - 2m{v_z}\;\Omega \cos \lambda \;{\vec u_x}\)
By plugging in the velocity along (Oz) by its value when we suppose the Coriolis force to be zero, we get the order of magnitude of the Coriolis force :
\({\vec f_{ie}} = - 2m{v_z}\;\Omega \cos \lambda \;{\vec u_x} = (2m{g_0}\Omega \cos \lambda )\;t\;{\vec u_x}\)
The time of the fall \(t_f\) can be calculated by supposing the fall to be vertical :
\(t_f=\sqrt{2h/g_0}\)
The order of magnitude of the deviation, for \(h=100\;m\) and \(\lambda=45°\) is :
\(x=1,5\;cm\)