Bernoulli's equation
Complément : A video (in french) about Bernoulli's equation (with some fun science experiments)
Fondamental : In the case of a perfect, steady, irrotational, incompressible and homogeneous flow
It is assumed in the following that the only volume force (other than the pression forces) is the weight.
We study the case of a perfect, steady, irrotational, incompressible and homogeneous flow.
The Euler equation becomes :
\(\mu \;\overrightarrow {grad} \left( {\frac{{v^2 }}{2}} \right) = - \overrightarrow {grad} P\; + \mu \;\vec g\)
Noting : (the (Oz) axis is upward)
\(\mu \;\vec g = - \mu \;\overrightarrow {grad} (gz)\)
So :
\(\mu \;\overrightarrow {grad} \left( {\frac{{v^2 }}{2}} \right) = - \overrightarrow {grad} P\; - \mu \;\overrightarrow {grad} (gz)\)
Where :
\(\overrightarrow {grad} \left( {\mu \;\frac{{v^2 }}{2} + \mu \;gz + P} \right) = \vec 0\)
A scalar field whose gradient is zero is independent of the point \(M\) ; this is only a function of time \(f(t)\).
As the flow is stationary, this function is constant :
\(\frac{1}{2}\mu \;v^2 + \mu \;gz + P = Cste\)
This is Bernoulli's theorem, which states that the quantity \(\frac{1}{2}\mu \;v^2 + \mu \;gz + P\) remains in every point of the fluid equal to the same constant.
Remarque :
It is noted that \(\frac{1}{2}\mu v^2\) and \(\mu g z\) denote the kinetic and potential energies density (gravity), homogeneous to a pressure.
Remarque :
In the particular case \(v=0\), there is the hydrostatic law of fluid :
\(\mu \;gz + P = Cste\)
Attention : Bernoulli's equation for a perfect, steady, irrotational, incompressible and homogeneous flow
\(\frac{1}{2}\mu \;v^2 + \mu \;gz + P = Cste\)
The constant is the same for all points of the fluid.
Fondamental : For a perfect, stationary, incompressible and homogeneous flow
The Euler equation becomes now : (\(\overrightarrow {rot} \;\vec v\ne\vec 0\))
\(\mu \;(\overrightarrow {rot} \;\vec v \wedge \;\vec v) = - \overrightarrow {grad} \left( {\mu \;\frac{{v^2 }}{2} + \mu \;gz + P} \right)\)
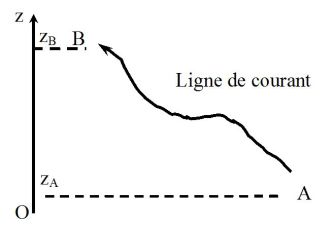
In order to eliminate the curl term, we do a dot product this term with \(d\vec r\) and we integrate it along the current line between points A and B :
\(\int_{\;A}^{\;B} {} \mu \;(\overrightarrow {rot} \;\vec v \wedge \;\vec v).d\vec r = - \int_{\;A}^{\;B} {} \overrightarrow {grad} \left( {\mu \;\frac{{v^2 }}{2} + \mu \;gz + P} \right).d\vec r\)
At any point, \(d\vec r\) is parallel to the velocity field and the term \( (\overrightarrow {rot} \;\vec v \wedge \;\vec v).d\vec r\) is null.
So :
\(\int_{\;A}^{\;B} {} \overrightarrow {grad} \left( {\mu \;\frac{{v^2 }}{2} + \mu \;gz + P} \right).d\vec r = 0\)
Either :
\(\frac{1}{2}\mu \;v_A^2 + \mu \;gz_A + P_A = \frac{1}{2}\mu \;v_B^2 + \mu \;gz_B + P_B\)
Thus, the abandonment of the "irrotational flow" hypothesis restricted Bernoulli's theorem at points \(A\) and \(B\) in the same current line.
Attention : Bernoulli's equation for a perfect, stationary, incompressible and homogeneous flow
The abandonment of the "irrotational flow" hypothesis restricted Bernoulli's theorem at points \(A\) and \(B\) in the same current line :
\(\frac{1}{2}\mu \;v_A^2 + \mu \;gz_A + P_A = \frac{1}{2}\mu \;v_B^2 + \mu \;gz_B + P_B\)
Remarque : Energetical interpretation of Bernoulli's equation
We are in the case of a perfect, steady, irrotational, incompressible and homogeneous flow. So :
\(\frac{1}{2}\mu \;v^2 + \mu \;gz + P = C\)
By multiplying with the volume \(d\tau\) of a fluid particle :
\(\frac{1}{2}\mu \;d\tau \;v^2 + \mu \;d\tau \;gz + P\;d\tau = Cste\)
We recognize :
\(\mu d\tau gz\) : gravitational potential energy of the fluid particle.
\(\frac{1}{2}\mu d\tau v^2\) : kinetic energy of the fluid particle.
\(Pd\tau\) : potential energy associated with the pressure forces.
Bernoulli's theorem, more general than the simple conservation of mechanical energy of a material point in a non-continuous medium, is a special case of the first law of thermodynamics :
\(d(U + E_{c,macro} + E_{p,macro} ) = - P\;d\tau + \delta Q\)
With \(dU=0\) and \(\delta Q=0\) : the implicit assumptions of the application of Bernoulli's theorem are isothermal and adiabatic aspects of evolution.
Indeed, for a perfect fluid, the internal energy depends only on the temperature.
Furthermore, the aspect of adiabatic transformation is not problematic ; in the absence of heat transfer from the outside of the fluid, there 's no heat within a non-viscous fluid.
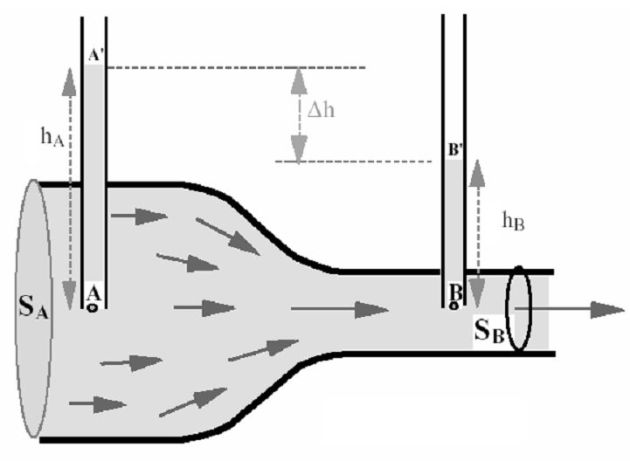
Complément : The phenomenon of Venturi
A homogeneous, steady, incompressible flow and subject only to pressure forces, is limited by a duct with variable section.
The problem is one-dimensional : all quantities have a uniform value on a straight section of the pipe.
The conservation of volume flow rate \(D_v\) between the two cross-sections \(S_A\) and \(S_B\) gives :
\(v_A S_A = v_B S_B\;\;\;\;\;\;so\;\;\;\;\;\;v_A<v_B\)
The application of the Bernoulli's theorem between two points \(A\) and \(B\) located on the same horizontal gives :
\(\frac{1}{2}\mu v_A^2 + P_A = \frac{1}{2}\mu v_B^2 + P_B\)
We deduce that \(P_A>P_B\) : the small section parts, so high speed, are also areas of low pressure (Venturi effect).
In the vertical tubes, the fluid is immobile and liquid heights measure pressures \(P_A\) and \(P_B\) :
\(P_A = P_{atm} + \mu gh_A \;\;\;\;\;\;\;\;\;\;and\;\;\;\;\;\;\;\;\;\;P_B = P_{atm} + \mu gh_B\)
We deduce the pressure difference :
\(P_A - \;P_B = \mu g(h_A - h_B )\)
Can then deduce the volume flow rate in the pipe, by calculating beforehand \(v_A\) :
\(v_A^2 - v_B^2 = v_A^2 - \left( {\frac{{S_A }}{{S_B }}} \right)^2 v_A^2 = \frac{2}{\mu }(P_B - P_A ) = - 2g(h_A - h_B )\)
Where :
\(v_A = \sqrt {\frac{{S_B^2 }}{{S_A^2 - S_B^2 }}2g(h_A - h_B )}\)
And the volumetric flow rate \(D_v\) is :
\(D_v = S_A v_A = S_A \sqrt {\frac{{S_B^2 }}{{S_A^2 - S_B^2 }}2g(h_A - h_B )}\)
The Venturi tube may also serve as a flow rate meter.
Remark :
The Venturi effect remains verified by a compressible gas such as air, as long as the speed remains below the velocity of sound propagation.