Flow of a viscous fluid on an inclined plane
Take 20 minutes to prepare this exercise.
Then, if you lack ideas to begin, look at the given clue and start searching for the solution.
A detailed solution is then proposed to you.
If you have more questions, feel free to ask them on the forum.
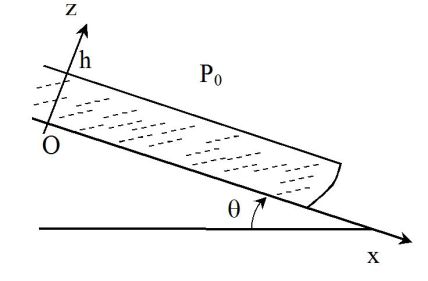
One consider a steady flow of layer of incompressible and viscous fluid, of height \(h\), on an inclined plane.
It is assumed one-dimensional flow : the velocity field is parallel to the axis Ox and will depend only on the variable\( z\).
At the free surface, the pressure is uniform and is \(P_0\).
The density of the fluid, assumed Newtonian, is \(\rho\) and its viscosity \(\eta\).
It will be recognized that because of the low viscosity of the air above the fluid, there is no shear stress at \(z = h\).
Given the Navier-Stokes equation for a Newtonian fluid :
\(\rho \left[ {\frac{{\partial \vec v}}{{\partial t}} + (\vec v.\overrightarrow {grad} )\vec v} \right] = - \overrightarrow {grad} P + \rho \vec g + \eta \Delta \vec v\)
Question
Simplify and project the Navier-Stokes.
Solution
In a permanent regime :
\(\frac{{\partial \vec v}}{{\partial t}} = \vec 0\)
Convective acceleration is equal to , with the hypotheses of the statement : (\(\vec v=v(z)\;\vec e_x\))
\((\vec v.\overrightarrow {grad} )\vec v = \left( {{v}(z).\frac{\partial }{{\partial x}}} \right){v}(z) = 0\)
Therefore :
\(- \overrightarrow {grad} P + \rho \vec g + \eta \Delta \vec v = \vec 0\)
Question
Determine the velocity field \(\vec v = v(z)\;\vec e_x\) by taking into account boundary conditions.
Solution
The previous equation gives, in projection ( and \(P\) does not depend on\( y\)) :
\(\frac{{\partial P}}{{\partial x}} = \rho g\sin \theta + \eta \frac{{{d^2}v}}{{d{z^2}}}\;\;\;\;\;\;\;;\;\;\;\;\;\;\;\frac{{\partial P}}{{\partial z}} = - \rho g\cos \theta\)
The second equation given by integration :
\(P(x,z) = - \rho g\cos \theta \;z + cste = \rho g\cos \theta (h - z) + {P_0}\)
The first becomes, noting that \(\frac{{\partial P}}{{\partial x}} = 0\) :
\(\rho g\sin \theta + \eta \frac{{{d^2}v}}{{d{z^2}}} = 0\;\;\;\;\;so\;\;\;\;\;v(z) = - \frac{{\rho g\sin \theta }}{{2\eta }}{z^2} + az + b\)
The velocity is zero at \(z = 0\) and the air does not exert tangential force on the liquid at \(z = h\), thus :
\(dv/dz=0\) at \(z=h\)
So :
\(v(z) = \frac{{\rho g\sin \theta }}{{2\eta }}(2h - z)z\)
A parabolic velocity profile with a maximum at \(z = h\) is obtained.
Question
We are interested in a wide flow \(L\) along the axis Oy, with \(L >> h\), in order to neglect edge effects.
Calculate the volume flow rate \(D_v\) and deduce the average fluid velocity.
Solution
The volumetric flow rate is :
\({D_v} = L\int_0^h {\frac{{\rho g\sin \theta }}{{2\eta }}(2h - z)z} \;dz = \frac{{\rho gL{h^3}\sin \theta }}{{3\eta }}\)
And the average velocity of the flow is :
\({v_{moy}} = \frac{{{D_v}}}{{Lh}} = \frac{{\rho g{h^2}\sin \theta }}{{3\eta }}\)
Question
We are interested in a layer of glycerin to which :
\(\rho = 900\ kg.m^{ - 3}\) and \(\eta = 0,85\ Pa.s\)
and of thickness \(1 \;mm\). The angle \(\theta\) is \(10°\).
Calculate the average speed and comment on the result using the Reynolds number.
Solution
We get :
\(v_{moy}=0,61\;mm.s^{-1}\)
And the Reynolds number is :
\(R_e = \frac {\rho h v_{moy}}{\eta}=6,5\;10^{-4}<<1\)
Viscosity forces are sufficient to impose a field of laminar speeds.