Navier-Stokes equation
Complément :
Fondamental : Surface Forces of viscosity
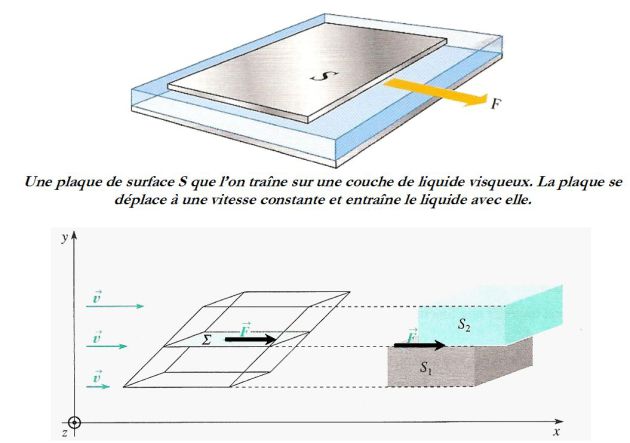
Studying a simple case in which the planes parallel to (Oxz) slide on each other (see figures).
This case is a good approximation of reality when the dimensions of the flow along (Ox) and (Oz) are big compared to the thickness of the fluid layer.
It is assumed that the velocity vector can be written as (see figure) :
\(\vec v=v(y,t)\;\vec u_x\)
Since \(div(\vec v) = 0\), this flow can be that of an incompressible fluid.
Consider two fluid elements \((S_1)\) and \((S_2)\), separated by the surface \((\Sigma)\), of area \(S\) and perpendicular to (Oy).
The shear force exerted by \((S_2)\) on \((S_1)\), is tangent to \((\Sigma )\).
In the case of the figure, the surface \((S_2)\) is faster than the surface \((S_1)\) and thus takes the fluid with it.
This force is :
Proportional to the area \(S\) of the surface \((\Sigma )\).
The same direction as \(\vec u_x\) if \(v(y,t)\) is an increasing function of \(y\).
To a fluid called "Newtonian", the shearing force is a linear function of the derivative \(\frac{{\partial v(y,t)}}{{\partial y}}\).
Finally, for unidirectional flow, such that \(\vec v=v(y,t)\;\vec u_x\), the force of tangential surface \(\vec F\), known as shear force or viscosity force, which is exerted through a normal area of surface \(S\) to \(\vec u_y \) (it is the force exerted by the upper layer on the lower layer) is expressed as :
\(\vec F = \eta \frac{{\partial v(y,t)}}{{\partial y}}S\;\vec u_x\)
The viscosity has the effect, in a unidirectional flow, to accelerate the slow elements and to slowdown fast elements.
It is therefore an internal transfer of momentum, which has the characteristics of diffusion of momentum.
The coefficient \(\eta\), called coefficient of viscosity of the fluid may be, with a good approximation, considered as a constant characteristic of the fluid at a given temperature.
The unit for viscosity coefficient is the Poiseuille (symbol \(Pl\), equal to \(1\) \(Pa.s\)).
Some examples (in normal conditions) :
Corps pur | Eau | Air | Glycérine |
Viscosité (Pl) | \(1,0.10^{-3}\) | \(1,0.10^{-5}\) | \(1,4\) |
Attention : Surface Forces of viscosity
For unidirectional flow, such that :
\(\vec v=v(y,t)\;\vec u_x\)
The force of a tangential surface \(\vec F\), known as shear force or viscosity force, which is exerted through a normal area of surface \(S\) to \(\vec u_y \) (it is the force exerted by the upper layer on the lower layer) is expressed so :
\(\vec F = \eta \frac{{\partial v(y,t)}}{{\partial y}}S\;\vec u_x\)
Fondamental : Volume equivalence of viscous forces
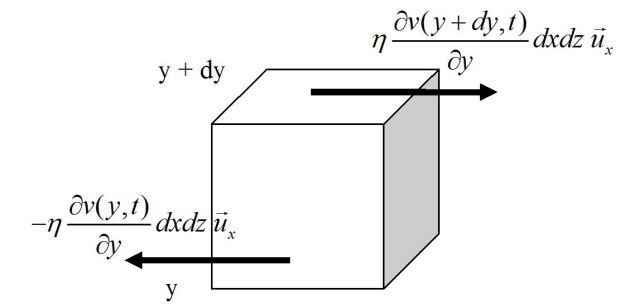
Consider a "pad" of fluid of volume \(d\tau=dxdydz\).
It is assumed that the velocity field can also be written as :
\(\vec v=v(y,t)\;\vec u_x\)
For such a field, the viscous forces are on the (Ox) axis and only the faces \(y\) and \(y+dy\) are concerned.
We can write, applying the law of action and reaction, the resultant viscosity forces on the pad of fluid :
\(d\vec F_{vis} = d\vec F_{vis} (y + dy) + d\vec F_{vis} (y) = \eta \frac{{\partial v(y + dy,t)}}{{\partial y}}\;dx\;dz\;\vec u_x - \eta \frac{{\partial v(y,t)}}{{\partial y}}\;dx\;dz\;\vec u_x\)
Either :
\(d\vec F_{vis} = \eta \frac{{\partial ^2 v(y,t)}}{{\partial y^2 }}\;dx\;dy\;dz\;\vec u_x \;\;\;\;\;\;\;\;\;\;so \;\;\;\;\;\;\;\;\;\;\vec f_{vis} = \frac{{d\vec F_{vis} }}{{d\tau }} = \eta \frac{{\partial ^2 v(y,t)}}{{\partial y^2 }}\;\vec u_x \;\)
For a field of any speed but corresponding to an incompressible flow, we assume that this result can be generalized in the form :
\(\vec f_{vis} = \frac{{d\vec F_{vis} }}{{d\tau }} = \eta \;\Delta \vec v = \eta \left| \begin{array}{l}\Delta v_x \\\Delta v_y \\\Delta v_z \\\end{array} \right|\)
Where we have introduced the laplacian \(\Delta \vec v\) of vector field \(\vec v\).
\(\vec f_{vis}\) is the volumetric density of the viscous forces ; it is only a mathematical equivalent because these forces apply only to the surface of a system.
Attention : Volume equivalence of viscous forces
For a field of any speed but corresponding to an incompressible flow, the volume density of viscous forces is :
\(\vec f_{vis} = \frac{{d\vec F_{vis} }}{{d\tau }} = \eta \;\Delta \vec v = \eta \left| \begin{array}{l}\Delta v_x \\\Delta v_y \\\Delta v_z \\\end{array} \right|\)
Fondamental : Navier-Stokes equation
The Newton's second law applied to a particle of fluid, taking into account the viscosity force leads to the Navier – Stokes equation :
\(\rho \left[ {\frac{{\partial \vec v}}{{\partial t}} + \left( {\vec v.\overrightarrow {grad} } \right)\vec v} \right] = - \overrightarrow {grad} P + \rho \vec g + \eta \Delta \vec v\)
It is the Navier – Stokes' equation.
Or :
\(\rho \left[ {\frac{{\partial \vec v}}{{\partial t}} + \overrightarrow {rot} \vec v \wedge \vec v + \frac{1}{2}\overrightarrow {grad} (v^2 )} \right] = - \overrightarrow {grad} P + \rho \vec g +\eta \Delta \vec v\)
Let's recall that :
Incompressible fluid : \(div (\vec v)=0\)
\(\rho=cste\)
The condition for the speed in the fluid - solid interface is :
\(\vec v_{fluid} - \vec v_{solide}=\vec 0\)
Attention : Navier-Stokes equation
\(\rho \left[ {\frac{{\partial \vec v}}{{\partial t}} + \left( {\vec v.\overrightarrow {grad} } \right)\vec v} \right] = - \overrightarrow {grad} P + \rho \vec g + \eta \Delta \vec v\)
It is the Navier - Stokes.
Or :
\(\rho \left[ {\frac{{\partial \vec v}}{{\partial t}} + \overrightarrow {rot} \vec v \wedge \vec v + \frac{1}{2}\overrightarrow {grad} (v^2 )} \right] = - \overrightarrow {grad} P + \rho \vec g +\eta \Delta \vec v\)