In physics, the term field denotes a physical quantity that is continuous function of position, within a certain region of space.

We distinguish scalar fields (such as temperature or electrostatic potential) from vector fields (such as the velocity of a moving fluid or the electric field \(\vec E\)).

A vector field assigns a direction, as well as a magnitude, to each point in space.

Since a vector can be represented by three components, a vector field is specified analytically by a set of three functions of position.

Since scalar and vector fields are functions of positions, they must have spatial derivatives and integrals.

We consider first a scalar field \(\phi (x,y,z)\).

The rate of change in \(\phi\) for small step away from the point \((x,y,z)\) depends upon the direction of the step : the derivative operation has vectorlike properties.

Specifically, for an infinitesimal step of magnitude \(ds\) in the direction specified by the unit vector \(\vec n\) :

\(ds\;\vec n = dx \;\vec u_x+dy\;\vec u_y +dz\;\vec u_z\)

The change in \(\phi\) is :

\(d\phi = \frac{{\partial \phi }}{{\partial x}}dx + \frac{{\partial \phi }}{{\partial y}}dy + \frac{{\partial \phi }}{{\partial z}}dz\)

And :

\(d\phi = \left( {\frac{{\partial \phi }}{{\partial x}}{{\vec u}_x} + \frac{{\partial \phi }}{{\partial y}}{{\vec u}_y} + \frac{{\partial \phi }}{{\partial z}}{{\vec u}_z}} \right).ds\;\vec n = \left( {\overrightarrow {grad} \phi } \right).ds\;\vec n\)

Where we introduce the gradient (or Nabla \(\vec \nabla\)) operator :

\(\overrightarrow {grad} = \vec \nabla = \frac{\partial }{{\partial x}}{{\vec u}_x} + \frac{\partial }{{\partial y}}{{\vec u}_y} + \frac{\partial }{{\partial z}}{{\vec u}_z}\)

Thus the derivated of \(\phi\) in the direction \(\vec n\) is :

\(\frac{{d\phi }}{{ds}} = \vec n.\overrightarrow {grad} \phi\)

The vector field \(\overrightarrow {grad} \phi \) is the gradient of \(\phi\) :

\(\overrightarrow {grad} \phi = \vec \nabla \phi = \frac{{\partial \phi }}{{\partial x}}{{\vec u}_x} + \frac{{\partial \phi }}{{\partial y}}{{\vec u}_y} + \frac{{\partial \phi }}{{\partial z}}{{\vec u}_z}\)

The gradient is thus a vector derivative, having the magnitude and direction of the greatest space rate of change of the scalar field \(\phi\).

The derivative in an arbitrary direction is simply the component of the gradient vector in that direction.

The gradient is directed perpendicular to the surface \(\phi=cste\).

If the field is expressed in cylindrical or spherical coordinate systems, the forms of derivatives are altered but the meaning of the gradient is unchanged.

• Cylindrical coordinate system :

  \(\overrightarrow {grad} \phi = \vec \nabla \phi = \frac{{\partial \phi }}{{\partial r}}{{\vec u}_r} + \frac{1}{r}\frac{{\partial \phi }}{{\partial \theta }}{{\vec u}_\theta } + \frac{{\partial \phi }}{{\partial z}}{{\vec u}_z}\)

• Spherical coordinate system :

  \(\overrightarrow {grad} \phi = \vec \nabla \phi = \frac{{\partial \phi }}{{\partial r}}{{\vec u}_r} + \frac{1}{r}\frac{{\partial \phi }}{{\partial \theta }}{{\vec u}_\theta } + \frac{1}{{r\sin \theta }}\frac{{\partial \phi }}{{\partial \varphi }}{{\vec u}_\varphi }\)

The divergence of a vector field :

\(\vec A(\vec r)=A_x\vec u_x+A_y\vec u_y+A_z\vec u_z\)

is defined by (in a cartesian coordinate system) :

\(div\vec A(\vec r) = \vec \nabla .\vec A(\vec r) = \frac{{\partial {A_x}}}{{\partial x}} + \frac{{\partial {A_y}}}{{\partial y}} + \frac{{\partial {A_z}}}{{\partial z}}\)

It can be proved that the divergence is the flux generation per unit volume.

• Cylindrical coordinate system :

  \(div\vec A = \frac{1}{r}\frac{{\partial (r{A_r})}}{{\partial r}} + \frac{1}{r}\frac{{\partial ({A_\theta })}}{{\partial \theta }} + \frac{{\partial ({A_z})}}{{\partial z}}\)

• Spherical coordinate system :

  \(div\vec A = \frac{1}{{{r^2}}}\frac{{\partial ({r^2}{A_r})}}{{\partial r}} + \frac{1}{{r\sin \theta }}\frac{{\partial (\sin \theta \;{A_\theta })}}{{\partial \theta }} + \frac{1}{{r\sin \theta }}\frac{{\partial ({A_\phi })}}{{\partial \phi }}\)

Green-Ostrogradsky theorem :

\(\iiint_{(V)}div(\vec A(\vec r).d\tau = \oiint_{(S)}\vec A.\vec n dS\)

Where the finite closed surface \((S)\) surrounds the finite volume \((V)\).

The curl of a vector field is defined by (in a cartesian coordinate system) :

\(\overrightarrow {rot} \vec A(\vec r) = \vec \nabla \wedge \vec A(\vec r)\)

It means :

\(\overrightarrow {rot} \;\vec A = \vec \nabla \wedge \vec A = \left[ \begin{array}{l}\frac{\partial }{{\partial x}} \\\frac{\partial }{{\partial y}} \\\frac{\partial }{{\partial z}} \\\end{array} \right] \wedge \left[ \begin{array}{l}{A_x} \\{A_y} \\{A_z} \\\end{array} \right] = \left[ \begin{array}{l}\frac{{\partial {A_z}}}{{\partial y}} - \frac{{\partial {A_y}}}{{\partial z}} \\- \frac{{\partial {A_z}}}{{\partial x}} + \frac{{\partial {A_x}}}{{\partial z}} \\\frac{{\partial {A_y}}}{{\partial x}} - \frac{{\partial {A_x}}}{{\partial y}} \\\end{array} \right]\)

• Cylindrical coordinate system :

  \(\overrightarrow {rot} \vec A(\vec r) = \left( {\frac{1}{r}\frac{{\partial {A_z}}}{{\partial \theta }} - \frac{{\partial {A_\theta }}}{{\partial z}}} \right){{\vec u}_r} + \left( {\frac{{\partial {A_r}}}{{\partial z}} - \frac{{\partial {A_z}}}{{\partial r}}} \right){{\vec u}_\theta } + \frac{1}{r}\left( {\frac{{\partial (r{A_r})}}{{\partial r}} - \frac{{\partial {A_r}}}{{\partial \theta }}} \right){{\vec u}_z}\)

• Spherical coordinate system :

  \(\overrightarrow {rot} \vec A(\vec r) = \left( {\frac{1}{{r\sin \theta }}\frac{{\partial ({A_\varphi }\sin \theta )}}{{\partial \theta }} - \frac{1}{{r\sin \theta }}\frac{{\partial {A_\theta }}}{{\partial \varphi }}} \right){{\vec u}_r} + \left( {\frac{1}{{r\sin \theta }}\frac{{\partial {A_r}}}{{\partial \varphi }} - \frac{1}{r}\frac{{\partial (r{A_\varphi })}}{{\partial r}}} \right){{\vec u}_\theta } + \left( {\frac{1}{r}\frac{{\partial (r{A_\theta })}}{{\partial r}} - \frac{1}{r}\frac{{\partial {A_r}}}{{\partial \theta }}} \right){{\vec u}_\varphi }\)

Stokes' theorem :

\(\iint_{(S)}\overrightarrow {rot} \vec A(\vec r).\vec n\;dS=\oint_{(C)}\vec A(\vec r).d\vec \ell\)

Where the closed loop \((C)\) bounds the finite open surface \((S)\).

The laplacian of a scalar field \(\phi (x,y,z)\) is defined by :

\(\Delta = \vec \nabla .\vec \nabla = {\vec \nabla ^2}\;\;\;\;\;thus\;\;\;\;\;\Delta \phi (x,y,z) = div(\overrightarrow {grad} \phi )\)

In a cartesian coordinate system :

\(\;\Delta \phi = \frac{{{\partial ^2}\phi }}{{\partial {x^2}}} + \frac{{{\partial ^2}\phi }}{{\partial {y^2}}} + \frac{{{\partial ^2}\phi }}{{\partial {z^2}}}\)

We can illustrate the terms of divergence and curl for some types fields : (see figure below)

The divergence and the curl are zero for the field whose field lines are parallel.

The divergence is negative for fields whose field lines converge to a point. It is positive for a diverging field.

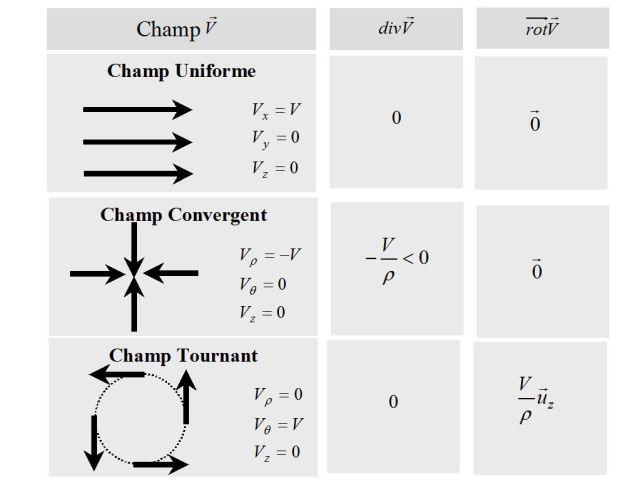
The curl operator of the last field (fields lines rotate around point O in the positf side) is positif.

The considered field can be that of velocity of a solid rotating about the(Oz) axis .

The speed of a point of the solid is, if \(\vec \Omega=\Omega \vec u_z\) denotes the rotation vector of the solid,, \(\vec v(M) = \vec \Omega \wedge \overrightarrow {OM}\).

Using Cartesian coordinates :

\(\overrightarrow {rot} \vec v = 2\vec \Omega\)

This result allows to associate the curl operator to the idea of rotation.