Flow viscometer
Take 20 minutes to prepare this exercise.
Then, if you lack ideas to begin, look at the given clue and start searching for the solution.
A detailed solution is then proposed to you.
If you have more questions, feel free to ask them on the forum.
A viscous, incompressible fluid, flows slowly from a cylindrical container of diameter \(D\) into a horizontal capillary tube of diameter \(d\) and length \(L\).
We neglect the effects due to the tube ends.
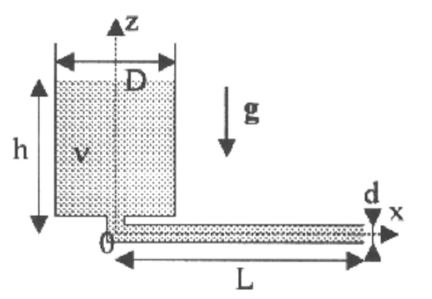
Question
Can we consider the flow as quasi-permanent ? Justify.
Deduce the expression of the volume flow rate \(D_v\) as a function of \(h\).
Solution
We place ourselves in the ARQS.
One has a cylindrical Poiseuille flow :
\(D_v = \frac{{\pi d^4 }}{{128\eta }}\frac{{P_e - P_s }}{L}\)
The liquid is practically at rest in the container of diameter \(D\).
We can therefore write the fluid static law :
\(P_s = P_0\) and \(P_e = P_0 + \mu gh\)
Consequently :
\(D_v = \frac{{\pi d^4 }}{{128\nu }}\frac{{gh}}{L}\)
With \(\nu = \frac{\eta }{\mu }\).
Question
Establish a differential equation satisfied by \(h (t)\).
Solve for the initial condition \(h (0) = h_0\).
Solution
The flow is incompressible, there is conservation of volume flow rate :
\(- S\frac{{dh}}{{dt}} = D_v\)
Either :
\(- \frac{{\pi D^2 }}{4}\frac{{dh}}{{dt}} = \frac{{\pi d^4 }}{{128\nu }}\frac{{gh}}{L}\)
This leads to the differential equation :
\(\frac{{dh}}{{dt}} + \frac{{gd^4 }}{{32\nu LD^2 }}h = 0\)
Whose solution is :
\(h(t) = h_0 e^{ - t/\tau }\)
With :
\(\tau =\frac{32\nu LD^2}{{{gd^4 } }}\)
Question
It took a duration \(t_0 = 75 \;min\) so that the liquid level moves from the height \(h_0=5\;cm\) to the height \(h_1=2,5\;cm\).
Determining the kinematic viscosity of the liquid.
It gives : \(D = 5 \;cm\), \(L = 40 \;cm\), \(d = 1 \;mm\) and \(g = 9,8 \;m.s^{-2}\)
Solution
Numerical application gives :
\( \nu = 2.10^{ - 6} \;m^2 .s^{ - 1}\)