Oscillations in a U-tube
Take 15 minutes to prepare this exercise.
Then, if you lack ideas to begin, look at the given clue and start searching for the solution.
A detailed solution is then proposed to you.
If you have more questions, feel free to ask them on the forum.
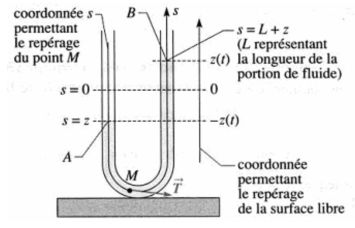
The oscillations of an incompressible fluid is studied in a small cross section of the U-tube.
It is assumed that the free surfaces remain in the rectilinear and vertical portions of the tube.
It is desired to determine the oscillation period of the liquid in the tube.
Question
First method : by applying Bernoulli's theorem in a regime depending on the time.
Solution
The cote of the free surface of fluid in the right branch of the tube is denoted \(z\).
The fluid is incompressible, the speed at any point \(M\) is :
\(\vec v(M,t) = \dot z \vec T\)
It integrates the Euler equation of a current line :
\(\mu \int_A^B {\frac{{\partial \vec v(M,t}}{{\partial t}}.d\vec \ell = - \left[ {\mu gz(M,t) + \frac{1}{2}\mu {v^2}(M,t) + P(M,t)} \right]} _A^B\)
Either, noting \(L\) the liquid length :
\(L\ddot z = - 2gz\)
Either :
\(\ddot z = - 2\frac{g}{L}z = - \omega _0^2z\;\;\;\;\;\;(\omega _0^2 = 2\frac{g}{L})\)
The period is then :
\(T = \frac{{2\pi }}{{{\omega _0}}} = 2\pi \sqrt {\frac{L}{{2g}}}\)
Question
Second method : by performing an energy balance.
Solution
The kinetic energy of all of the fluid is : (\(s\) is the U-tube cross section)
\({E_c} = \frac{1}{2}\mu sL{\dot z^2}\)
The potential energy is divided into three parts : it is assumed that at time \(t = 0\), the drop was \(h\) (the left side is lowered \(h\) relative to the equilibrium position).
So (the center of mass is in the middle of the column of a considered fluid) :
\({E_p} = \mu s(h - z)g\frac{1}{2}(h - z) + \mu s(h + z)g\frac{1}{2}(h + z) + cste = \frac{1}{2}\mu sg{(h - z)^2} + \frac{1}{2}\mu sg{(h + z)^2} + cste\)
By derivation :
\(\mu L\ddot z - \mu g(h - z) + \mu g(h + z) = 0\)
Either :
\(\ddot z = - 2\frac{g}{L}z = - \omega _0^2z\)
We find the same equation.