Fluid Mechanics

The complexity of the Navier - Stokes equation :

\(\rho \left[ {\frac{{\partial \vec v}}{{\partial t}} + \left( {\vec v.\overrightarrow {grad} } \right)\vec v} \right] = - \overrightarrow {grad} P + \rho \vec g + \eta \Delta \vec v\)

is mainly due to two terms :

• The convection term of momentum \((\vec v.\overrightarrow {grad} )\vec v\), which makes the non-linear equation.

• The viscous diffusion term \(\eta \Delta \vec v\) due to the transfer of momentum, which introduces the second order derivative.

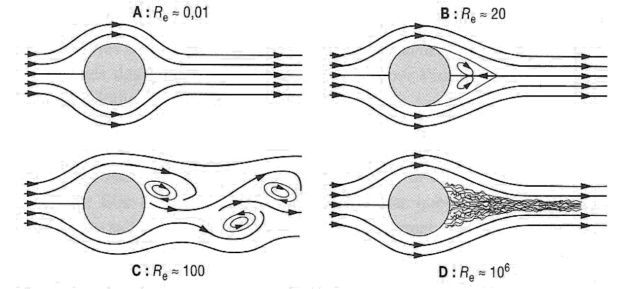
We consider a flow whose parameters are \(U_{\infty}\) (velocity of the fluid away from the obstacle) and \(D\) a characteristic size (length of the obstacle, for example).

The magnitude of the ratio between convective term and the diffusion term is :

\(\frac{{\left\| {\rho (\vec v.\overrightarrow {grad} )\vec v} \right\|}}{{\left\| {\eta \Delta \vec v} \right\|}} \approx \frac{{\rho \frac{{U_\infty ^2 }}{D}}}{{\eta \frac{{U_\infty }}{{D^2 }}}} = \frac{{\rho D U_\infty }}{\eta }\)

With \(\nu = \frac{\eta }{\rho }\) (\(\eta\) is the dynamic viscosity of fluid and \(\nu\) its kinematic viscosity) :

\(\frac{{\left\| {\rho (\vec v.\overrightarrow {grad} )\vec v} \right\|}}{{\left\| {\eta \Delta \vec v} \right\|}} \approx \frac{{D U_\infty }}{\nu } = R_e\)

\(R_e\) is the Reynolds number.

Experience shows that if \(R_e<2\;000\), the flow is laminar while if \(R_e>4\;000\), it easily becomes turbulent.

For a high Reynolds number, the transfer of momentum by convection are larger than those by diffusion ; this means that the characteristic time associated with the transfer by convection is shorter than that by diffusion.

It is as if the viscosity of the fluid was zero.

The fluid has a perfect fluid behavior and its motion is governed by the Euler equation :

\(\rho \;\frac{{\partial \vec v}}{{\partial t}} + \rho \;(\vec v.\overrightarrow {grad} )\;\vec v = - \overrightarrow {grad} P\; + \vec f_v\)

The thickness of the boundary layer \(\delta \approx \frac{L}{{\sqrt {R_e } }}\) is then low.

For a low Reynolds number, the momentum transfers by diffusion are greater than those by convection ; the characteristic time associated with the transfer by diffusion is shorter than by convection.

The Navier-Stokes' equation becomes :

\(\rho \;\frac{{\partial \vec v}}{{\partial t}} = - \overrightarrow {grad} P\; + \vec f_v + \eta \Delta \vec v\)

Flows dominated by the viscosity are still very low flows with a very short characteristic length (sap in the pores of trees) or involving highly viscous fluids (lava flows).

The convective term is non-linear : the apparition of turbulence occurs for high Reynolds numbers, so the nonlinear term clearly is greater than the linear term (due to the diffusive aspect of the flow, that is to say the viscosity).

So it is the non-linear aspect of the flow that promotes turbulence.