Poiseuille flow
Complément : A video (in french) about Poiseuille's flow (with some fun science experiments)
Fondamental : Velocity Fields and pressures
In 1835 a French physicist Poiseuille made a series of experiments to determine how a viscous fluid flows in a straight pipe.
His goal was to understand the dynamics of blood flow in humans knowing that the blood plasma behaves like a Newtonian fluid.
A density of incompressible viscous fluid \(\rho\) flows through a cylindrical tube of length \(L\) and radius \(R\).
The pressure at the input of the tube (\(z=0\)) is \(P_E\).
The pressure at the output of the tube (\(z=L\)) is \(P_S\).
We will calculate the velocity and pressure fields within the tube being placed in the steady state.
Laminar flow is assumed :
\(\vec v =v(r)\; \vec u_z\)
It is assumed that \(P=P(r,z)\) (invariance by rotation about the axis Oz) and the gravity is neglected.
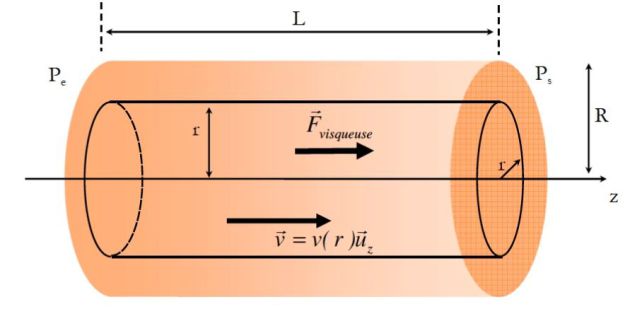
Applying the second law of Newton to a system consisting of the fluid contained in the cylinder of radius \(r<R\) at time \(t\) and the mass \(dm_1=dm\) that enters the cylinder between \(t\) and \(t+dt\).
At the moment \(t+dt\), this system is made up of fluid in the cylinder of radius \(r\) at \(t+dt\) and the same mass \(dm_2=dm\) that exits between \(t\) and \(t+dt\) (incompressible flow).
In the case of steady state, the change in momentum of the system is then simply zero :
\((P_e \pi r^2 \vec u_z - P_s \pi r^2 \vec u_z ) + \left( {\eta \frac{{dv}}{{dr}}2\pi rL\vec u_z } \right) = \vec 0\)
Where :
\(\frac{{dv}}{{dr}} = - \frac{{P_e - P_s }}{{2\eta L}}r\)
By integration, taking account of \(v(R)=0\) :
\(v(r)=\frac {\Delta P}{4 \eta L}(R^2-r^2)\)
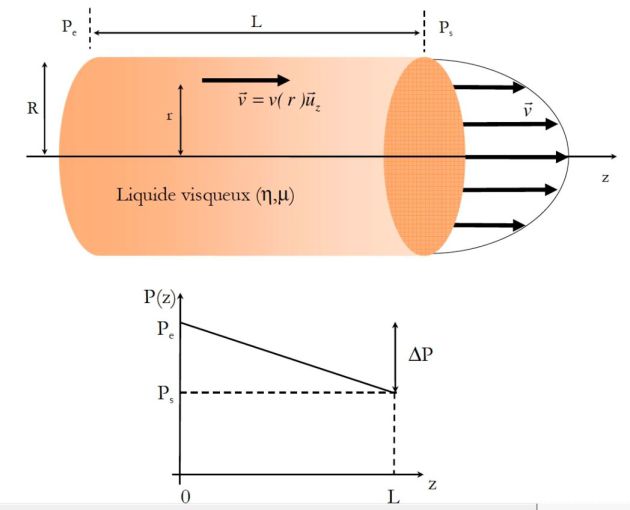
This gives the velocity profile in a Poiseuille flow.
The graph above shows the parabolic profile of the velocity field and the variation of the pressure.
Called "charge loss" the amount \(\Delta P=P_E-P_S\).
Fondamental : Volumetric flow rate
The volumetric flow rate is here :
\(D_v = \int_0^R {v(r)2\pi rdr} = \int_0^R {\frac{{\Delta P}}{{4\eta L}}(R^2 - r^2 )2\pi rdr}\)
Either :
\(D_v = \frac{{\Delta P}}{{\eta L}}\frac{\pi }{8}R^4\)
We define a "hydraulic resistance", by analogy with an ohmic resistor (\(\Delta U=V_1-V_2=RI\)) :
\(\Delta P=P_E-P_S=R_{hyd}D_v\)
Either :
\(R_{hyd}=\frac {8\eta L}{\pi R^4}\)
The hydraulic resistance is as much higher as the viscosity of the fluid is large and the radius of the tube is small.
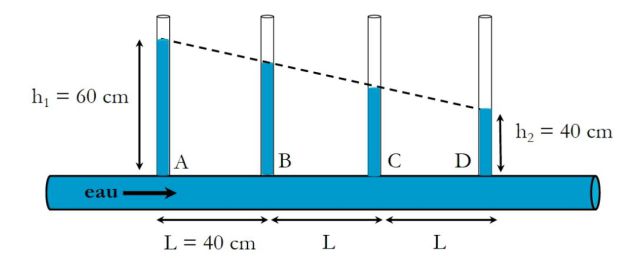
Exemple : Charge loss and hydraulic resistance
Placing a succession of vertical tubes along the pipe.
The measurement of water levels used to determine the pressure drop :
\(\Delta P=\mu _{eau} g (h_1-h_2)=2.10^3\;Pa\)
If the flow rate is \(D_v=10\;cm^3.s^{-1}=10^{-5}\;m^3.s^{-1}\), the hydraulic resistance can be deduced as :
\(R_{hyd}=\frac {\Delta P}{D_v}=2.10^8\;Pa.s.m^{-3}\)