Un sismographe
Consacrer 15 minutes de préparation à cet exercice.
Puis, si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Si vous avez des questions complémentaires, n'hésitez pas à les poser sur le forum.
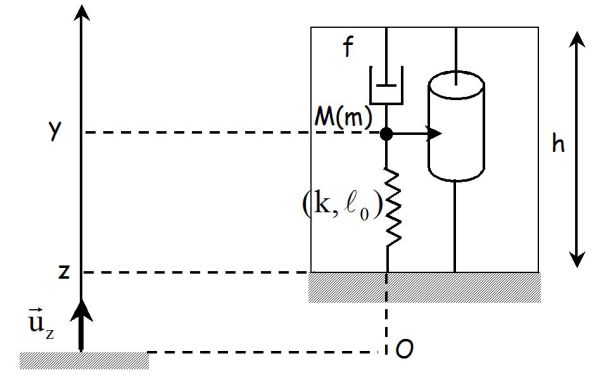
Un sismographe est constitué d'un ressort de raideur k et de longueur à vide \(\ell_0\), d'un amortisseur de coefficient de frottement \(f\) et d'une masse ponctuelle m.
Le ressort et l'amortisseur sont fixés à un cadre rigide ; un stylo reproduisant les déplacements verticaux de la masse m par rapport au cadre est fixé au niveau de la masse m.
Le cadre est mis en mouvement vertical sinusoïdal :
\(z(t)=Z_mcos(\omega t)+z_{eq}\)
Avec \(z_{eq}=0\).
Le référentiel Rg(O,z) est supposé galiléen.
Question
Déterminer l'équation différentielle vérifiée par la grandeur x, écart entre la longueur du ressort \(\ell\) à un instant t et sa longueur à l'équilibre \(\ell_{eq}\) (obtenu lorsque \(z=z_{eq}=0\)).
On fera apparaître le facteur de qualité Q du système ainsi que sa pulsation propre \(\omega_0\).
Question
Déterminer, en régime forcé, l'amplitude \(X_m\) de l'oscillation de la masse ainsi que la phase à l'origine.
Question
Comment choisir Q pour que la bande de pulsation reproduite soit la plus grande possible et que l'écart entre \(X_m\) et \(Z_m\) soit au maximum de \(5\%\) ?