Quelques applications classiques
Fondamental : Oscillateur harmonique amorti par frottement fluide (régime libre)
Un oscillateur harmonique amorti par frottement fluide obéit à l'équation différentielle suivante (cas à une dimension) :
\(m\ddot x = - kx - hm\dot x\;\;\;\;\;soit\;\;\;\;\;\ddot x + h\dot x + \frac{k}{m}x = 0\)
On pose :
\({\omega _0} = \sqrt {\frac{k}{m}} \;\;\;\;\;;\;\;\;\;\;h = 2\lambda = 2\sigma {\omega _0} = \frac{{{\omega _0}}}{Q}\)
\(\sigma\) est le facteur d'amortissement de l'oscillateur et Q le facteur de qualité.
Alors :
\(\;\ddot x + 2\lambda \dot x + \omega _0^2x = \ddot x + 2\sigma {\omega _0}\dot x + \omega _0^2x = \ddot x + \frac{{{\omega _0}}}{Q}\dot x + \omega _0^2x = 0\)
On recherche des solutions de la forme exp(rt), avec r appartenant a priori au corps des complexes.
On aboutit au polynôme caractéristique :
\(r^2+2\sigma \omega_0 r+\omega_0^2=0\)
dont le discriminant est :
\(\Delta=4\omega_0^2(\sigma^2-1)\)
Différents régimes sont observés, selon les valeurs prises par \(\sigma\) (ou \(Q=1/2\sigma\)) :
régime pseudo-périodique : alors \(\sigma<1\)
Dans le cas où \(x(0)=x_0\) et la vitesse initiale nulle :
\(\begin{array}{l}x(t) = {x_0}{e^{ - \sigma {\omega _0}t}}\left( {\cos (\omega t) + \frac{{\sigma {\omega _0}}}{\omega }\sin (\omega t)} \right) \\x(t) = C{e^{ - \sigma {\omega _0}t}}\cos (\omega t - \phi ) \\C = x_0^{}\sqrt {1 + {{\left( {\frac{{\sigma {\omega _0}}}{\omega }} \right)}^2}} \;\;\;;\;\;\;\tan \phi = \frac{{\sigma {\omega _0}}}{\omega } \\\end{array}\)
Avec :
\(avec\;\omega = {\omega _0}\sqrt {1 - {\sigma ^2}} \)
la pseudo-pulsation.
On peut noter que le facteur de qualité \(Q\) donne l'ordre de grandeur du nombre de pseudo-oscillations visibles expérimentalement.
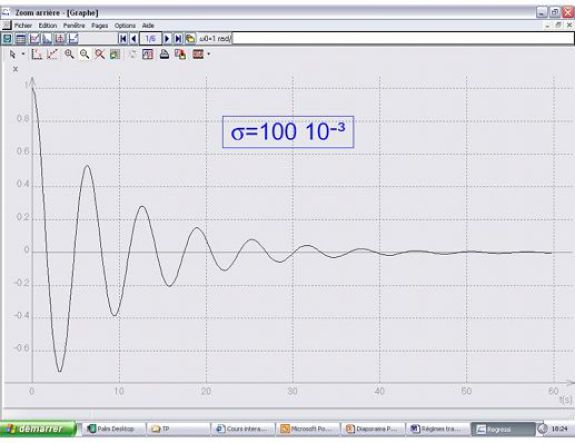
régime apériodique : alors \(\sigma>1\)
Dans le cas où \(x(0)=x_0\) et la vitesse initiale nulle :
\({r_1} = - \sigma {\omega _0} + {\omega _0}\sqrt {{\sigma ^2} - 1} \;;\;{r_2} = - \sigma {\omega _0} - {\omega _0}\sqrt {{\sigma ^2} - 1}\)
\(\begin{array}{l}\omega = {\omega _0}\sqrt {{\sigma ^2} - 1} \\x(t) = {x_0}{e^{ - \sigma {\omega _0}t}}\left( {ch(\omega t) + \frac{{\sigma {\omega _0}}}{\omega }sh(\omega t)} \right) \\x(t) = \frac{{{x_0}}}{2}{e^{ - \sigma {\omega _0}t}}\left( {\left( {1 - \frac{{\sigma {\omega _0}}}{\omega }} \right){e^{ - \omega t}} + \left( {1 + \frac{{\sigma {\omega _0}}}{\omega }} \right){e^{\omega t}}} \right) \\\end{array}\)
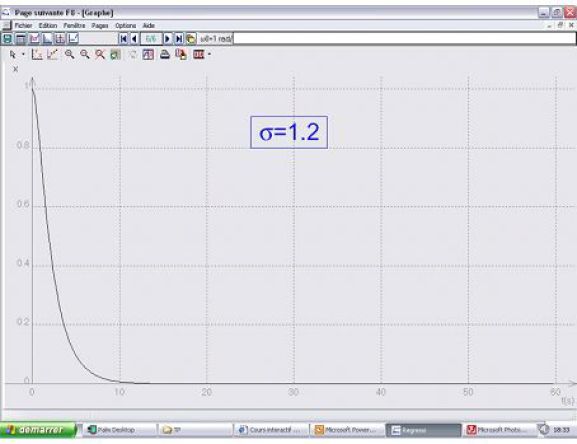
régime apériodique critique : alors \(\sigma=1\)
Dans le cas où \(x(0)=x_0\) et la vitesse initiale nulle :
\(x(t) = {x_0}(1 + {\omega _0}t){e^{ - {\omega _0}t}}\)
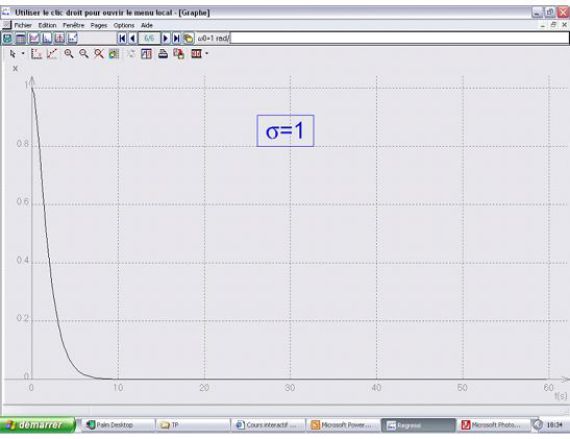
Régimes pseudo-périodique et apériodique
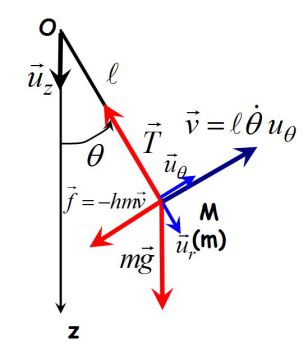
Fondamental : Le pendule simple
En présence d'une force de frottement fluide de la forme :
\(\vec f_v=-hm\vec v\)
Le PFD projeté sur le vecteur \(\vec u_{\theta}\) donne : (on peut aussi utiliser le théorème du moment cinétique)
\(m\ell \ddot \theta = - mg\sin \theta - hm(\ell \dot \theta )\)
Soit :
\(\ddot \theta + h\dot \theta + \frac{g}{\ell }\sin \theta = \ddot \theta + 2\sigma {\omega _0}\dot \theta + \omega _0^2\sin \theta = 0\)
Si l'angle \(\theta\) reste « petit », alors on retrouve l'équation habituelle :
\(\ddot \theta + h\dot \theta + \frac{g}{\ell }\theta = \ddot \theta + 2\sigma {\omega _0}\dot \theta + \omega _0^2\theta = 0\)
Exemple : Oscillateurs mécaniques en régime sinusoïdal forcé
Fondamental : Oscillateurs mécaniques en régime sinusoïdal forcé
Intérêt de l'étude :
L'analyse harmonique (ou fréquentielle) d'un système est son étude au moyen de sa réponse harmonique s(t), c'est-à-dire de sa réponse en régime permanent sinusoïdal lorsqu'il est soumis à une entrée sinusoïdale e(t) dont on fait varier la pulsation ω.
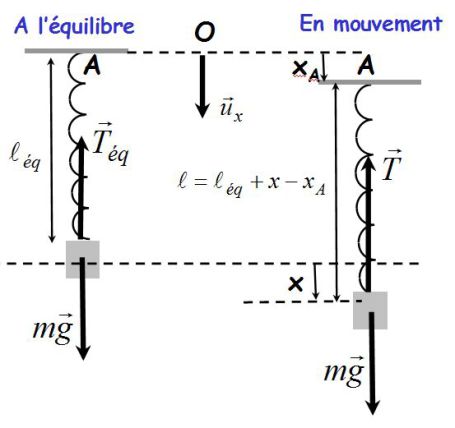
Modèle choisi : oscillateur mécanique vertical à point d'attache mobile
Le point d'attache du ressort est mobile en A.
Dans le référentiel galiléen du sol :
\(m\ddot x = mg - hm\dot x - k({\ell _{eq}} + x - {x_A} - {\ell _0})\)
En utilisant la condition d'équilibre :
\(\ddot x + h\dot x + \frac{k}{m}x = \frac{k}{m}{x_A}\)
Soit, avec les notations habituelles :
\(\ddot x + 2\sigma {\omega _0}\dot x + \omega _0^2x = \omega _0^2{x_A}\)
Dans la suite, on choisit :
\({x_A} = {X_{A,m}}\cos (\omega t)\)
Cette équation est formellement identique à celle vérifiée par la tension aux bornes d'un condensateur dans un circuit série (RLC) alimenté par un GBF (voir cours d'électricité) :
Si on note \(u_C\) la tension aux bornes du condensateur : (\(u_C=q/C\))
\(L\ddot q + R\dot q + \frac{1}{C}q = e(t)\)
Soit :
\({\ddot u_C} + \frac{R}{L}{u_C} + \frac{1}{{LC}}{u_C} = \frac{1}{{LC}}e(t)\)
Méthode de résolution par les nombres complexes (comme en électricité) :
On pose :
\({\underline x _A} = {X_{A,m}}{e^{i\omega t}}\;\;\;\;\;;\;\;\;\;\;\;\;\underline x = {X_m}{e^{i(\omega t + \phi )}}\;\;\;(x = {X_m}\cos (\omega t + \phi ))\)
Alors :
\(\underline {\dot x} = i\omega \underline x \;\;\;\;\;\;\;\;\;\;et\;\;\;\;\;\;\;\;\;\;\underline {\ddot x} = i\omega \underline {\dot x} = {(i\omega )^2}\underline x = - {\omega ^2}\underline x\)
Réponse en amplitude \(x(t)\) :
\(\begin{array}{l}\ddot x + 2\sigma {\omega _0}\dot x + \omega _0^2x = \omega _0^2{x_A} \\- \omega _{}^2\underline x + 2\sigma {\omega _0}(i\omega \underline x ) + \omega _0^2\underline x = \omega _0^2{\underline x _A} \\\left[ {(\omega _0^2 - \omega _{}^2) + 2i\sigma {\omega _0}\omega } \right]\;\underline x = \omega _0^2{\underline x _A} \\\end{array}\)
Soit :
\(\;\underline x = \frac{{\omega _0^2}}{{(\omega _0^2 - \omega _{}^2) + 2i\sigma {\omega _0}\omega }}{\underline x _A}\)
Ou encore :
\({X_m}{e^{i\phi }} = \frac{{\omega _0^2}}{{(\omega _0^2 - \omega _{}^2) + 2i\sigma {\omega _0}\omega }}{X_{A,m}}\)
L'amplitude maximale s'obtient en prenant le module de l'expression précédente :
\({X_m} = \frac{{\omega _0^2}}{{\sqrt {{{(\omega _0^2 - \omega _{}^2)}^2} + 4{\sigma ^2}\omega _0^2{\omega ^2}} }}{X_{A,m}}\)
\(X_m\) est maximale pour une pulsation qui vaut (et qui existe si \(\sigma <1/\sqrt{2}\)) :
\(\;\omega _r^{} = \omega _0^{}\sqrt {1 - 2{\sigma ^2}}\)
Et l'amplitude maximale à la « résonance d'amplitude » est :
\({X_m}({\omega _r}) = \frac{1}{{2\sigma \sqrt {1 - {\sigma ^2}} }}{X_{A,m}}\)
Les formules précédentes deviennent, en utilisant le facteur de qualité Q à la place du coefficient d'amortissement \(\sigma\) : (\(Q=1/2\sigma\)) :
\(\;\omega _r^{} = \omega _0^{}\sqrt {1 - \frac{1}{{2{Q^2}}}} \;\;\;\;\;\;\;\;\;\;avec\;\;\;\;\;\;\;\;\;\;Q > \frac{1}{{\sqrt 2 }}\)
Et :
\({X_m}({\omega _r}) = \frac{Q}{{\sqrt {1 - \frac{1}{{4{Q^2}}}} }}{X_{A,m}}\)
Remarque :
Pour de faibles amortissements (\(sigma\) "faible" et \(Q\) "grand"), alors :
\(\;\omega _r^{} \approx \omega _0^{}\;\;\;\;\;et\;\;\;\;\;{X_m}({\omega _r}) \approx Q{X_{A,m}}\)
Ainsi, si \(Q=10\), l'amplitude lors de la résonance vaut 10 fois celle de l'excitation : la résonance est dite «aiguë» et peut causer la destruction du système oscillant.
La figure précédente donne l'allure de \(X_m(\omega)\) pour différentes valeurs du facteur de qualité \(Q\).
On a choisi \(X_{A,m}=1\) et posé \(u=\omega/\omega_0\).
Plus Q est grand et plus la résonance est aigüe.
L'oscillateur constitue un filtre passe-bas, avec ou sans résonance.
Réponse en vitesse :
En notation réelle : \(v(t) = {V_m}\cos (\omega t + \psi )\)
En notation complexe : \(\underline v (t) = {V_m}{e^{i(\omega t + \psi )}}\)
En remarquant que \(\underline v = \underline {\dot x} = i\omega x\), il vient :
\(\;\underline v = i\omega \left( {\frac{{\omega _0^2}}{{(\omega _0^2 - \omega _{}^2) + 2i\sigma {\omega _0}\omega }}{{\underline x }_A}} \right) = \frac{{{\omega _0}}}{{i\left( {\frac{\omega }{{{\omega _0}}} - \frac{{{\omega _0}}}{\omega }} \right) + 2\sigma }}{\underline x _A}\)
Ou encore :
\({V_m}{e^{i\psi }} = \frac{{\omega _0^{}}}{{2\sigma + i\left( {\frac{\omega }{{{\omega _0}}} - \frac{{{\omega _0}}}{\omega }} \right)}}{X_{A,m}}\)
L'amplitude maximale de la vitesse \(V_m(\omega)\) s'obtient à partir du module :
\({V_m}(\omega ) = \frac{{\omega _0^{}}}{{\sqrt {4{\sigma ^2} + {{\left( {\frac{\omega }{{{\omega _0}}} - \frac{{{\omega _0}}}{\omega }} \right)}^2}} }}{X_{A,m}}\)
\(V_m(\omega)\) sera maximale (on parle alors de résonance de vitesse), si le dénominateur est minimal, c'est à dire pour une pulsation telle que :
\(\frac{\omega }{{{\omega _0}}} - \frac{{{\omega _0}}}{\omega } = 0\;\;\;\;\;\;\;\;\;\;\;soit\;\;\;\;\;\;\;\;\;\;\;\omega = {\omega _0}\)
L'amplitude de la vitesse valant alors :
\({V_m}({\omega _0}) = \frac{{\omega _0^{}}}{{2\sigma }}{X_{A,m}} = Q\omega _0^{}{X_{A,m}}\)
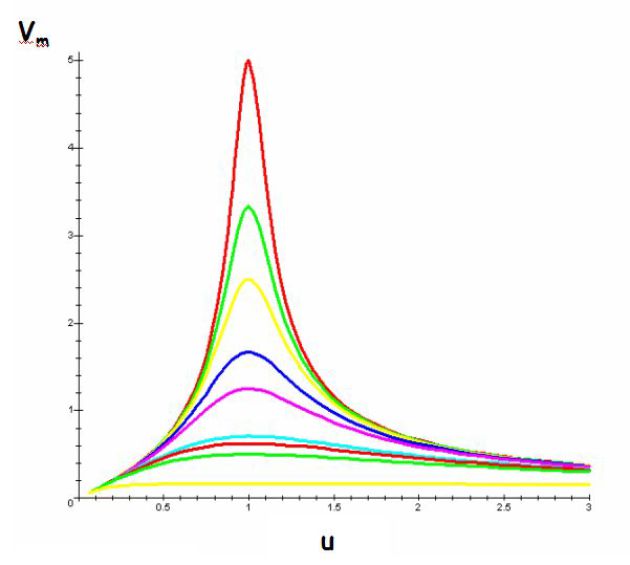
La figure précédente donne l'allure de \(V_m(\omega)\) pour différentes valeurs du facteur de qualité \(Q\).
On a choisi \(X_{A,m}=1\) et posé \(u=\omega/\omega_0\).
Plus Q est grand et plus la résonance est aigüe.
L'oscillateur constitue un filtre passe-bande.
Bande passante du filtre passe-bande :
C'est l'ensemble des pulsations ω pour lesquelles le gain en vitesse reste, par convention, supérieur au gain maximal (obtenu pour ω0) divisé par \(\sqrt{2}\).
La largeur de la bande passante vaut :
\(\Delta \omega = {\omega _{{c_2}}} - {\omega _{{c_1}}} = 2\sigma {\omega _0} = \frac{{{\omega _0}}}{Q}\)
Elle est d'autant plus faible (résonance aiguë) que l'amortissement est faible (et le facteur de qualité grand).