Le toboggan
Consacrer 10 minutes de préparation à cet exercice.
Puis, si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Si vous avez des questions complémentaires, n'hésitez pas à les poser sur le forum.
Un enfant assimilé à un point matériel G de masse m = 40 kg glisse sur un toboggan décrivant une trajectoire circulaire de rayon r = 2,5 m depuis la position θ = θ0 = 15° où il possède une vitesse nulle jusqu'à la position θ = 90° où il quitte le toboggan.
On néglige tous les frottements.
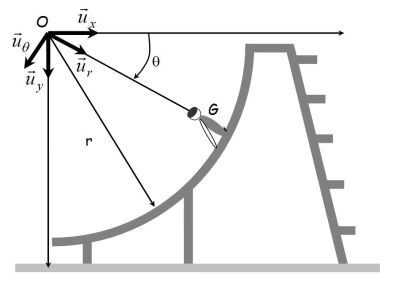
Question
Établir l'équation différentielle du mouvement de l'enfant en utilisant le théorème du moment cinétique puis en utilisant la conservation de l'énergie mécanique.
Solution
Le théorème du moment cinétique donne :
\(m{r^2}\ddot \theta {\vec u_z} = {\vec M_{poids/O}} = mgr\cos \theta {\vec u_z}\)
Soit :
\(\ddot \theta = \frac{g}{r}\cos \theta\)
L'énergie mécanique de l'enfant est :
\({E_m} = \frac{1}{2}m{r^2}{\dot \theta ^2} - mgr\sin \theta\)
Elle se conserve :
\(\frac{{d{E_m}}}{{dt}} = m{r^2}\dot \theta \ddot \theta - mgr\dot \theta \cos \theta\)
On retrouve bien la même équation différentielle.
Question
En déduire l'expression de la vitesse v de l'enfant en fonction de θ. Calculer la vitesse maximale atteinte par l'enfant. Commenter cette valeur.
Solution
L'intégrale première du mouvement :
\({E_m} = \frac{1}{2}m{v^2} - mgr\sin \theta = -mgr\sin {\theta _0}\)
Permet de déterminer la vitesse v :
\(v = \sqrt {2gr(\sin \theta - \sin {\theta _0})}\)
On peut aussi multiplier l'équation différentielle par \(\dot \theta\) puis intégrer. On obtient la même expression pour la vitesse \(v=r\dot \theta\).
La vitesse obtenue est trop importante : heureusement, les frottements permettent à l'enfant d'aller moins vite et de ne pas se blesser.