Ondes EM progressives dans le vide
Fondamental : Solution de l'équation de d'Alembert sous forme d'onde progressive
A une dimension, l'équation de d'Alembert s'écrit :
\(\frac{\partial^2s}{\partial z^2} - {\varepsilon _0}{\mu _0}\frac{{{\partial ^2}s}}{{\partial {t^2}}} = 0\;\;\;\;\;soit\;\;\;\;\;\frac{\partial^2s}{\partial z^2} - \frac{1}{{{c^2}}}\frac{{{\partial ^2}s}}{{\partial {t^2}}} = 0\;\;\;\;(\frac{1}{{{c^2}}} = {\varepsilon _0}{\mu _0})\)
où \(s(z,t)\) représente une des coordonnées du champ EM, fonction uniquement de \(z\) et de \(t\).
On démontre qu'une forme de solution de l'équation d'onde de d'Alembert s'écrit sous la forme :
\(s(z,t) = f(t - \frac{z}{c}) + g(t + \frac{z}{c})\)
où \(f\) est une fonction quelconque de la variable \(t-z/c\) et g une fonction de la variable \(t+z/c\).
Interprétation physique :
On considère une fonction de la forme :
\({s_ + }(z,t) = f(t - \frac{z}{c})\)
On constate que :
\(f(t - \frac{z}{c}) = f(t + \Delta t - \frac{{z + \Delta z}}{c})\)
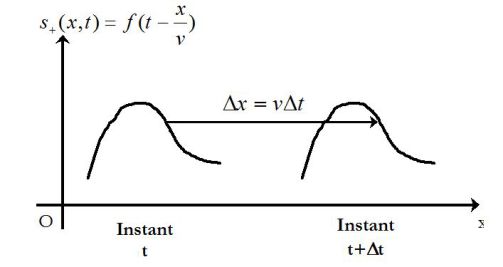
pour tout couple \(\Delta z\) et \(\Delta t\) vérifiant :
\(\Delta z=c\Delta t\)
Ainsi, \(s_+(z,t)\) représente un signal qui se propage sans déformation à la vitesse c le long de l'axe (Oz) dans le sens positif.
La solution :
\({s_ - }(z,t) = f(t + \frac{z}{c})\)
représente un signal qui se propage sans déformation à la vitesse c le long de l'axe (Oz) dans le sens négatif.
Dans un plan \(z=cste\), les fonctions \({s_ + }(z,t) = f(t - \frac{z}{c})\) et \({s_ - }(z,t) = f(t + \frac{z}{c})\) prennent, à tout instant, la même valeur : on parle d'onde plane et les plans \(z=cste\) sont appelés des plans d'onde.
Une source (par exemple, une station radiophonique) émet a priori des ondes sphériques ; cependant, à grande distance de celle-ci, l'onde reçue pourra être localement assimilée à une onde plane progressive
Ondes planes progressives monochromatiques (ou harmoniques, OPPH) :
L'équation de propagation est linéaire ; par conséquent, l'analyse de Fourier permet d'affirmer que toute solution de cette équation est la somme de fonctions sinusoïdales du temps.
On se limite ici à des solutions harmoniques de l'équation de d'Alembert, c'est-à-dire des solutions de la forme (pour une onde qui se propage dans le sens \(x>0\) :
\(s(z,t) = A\;\cos \left( {\omega (t - \frac{z}{c})} \right)\)
Ces solutions correspondent à des ondes planes progressives harmoniques (OPPH).
Ces fonctions, de période temporelle \(T=2\pi/\omega\) possèdent une période spatiale \(\lambda=cT\) appelée longueur d'onde.
On définit le vecteur d'onde \(\vec k\) tel que :
\(\vec k = k\;{\vec u_z}\;\;\;\;\;\;\;\;\;\;avec\;\;\;\;\;\;\;\;\;\;k = \frac{\omega }{c} = \frac{{2\pi }}{\lambda }\)
L'OPPH est alors de la forme :
\(s(z,t) = A\;\cos \left( {\omega t - kz)} \right)\)
En notation réelle, le champ électrique pourra s'écrire :
\(\vec E(z,t) = {\vec E_0}\cos (\omega (t - \frac{z}{c})) = {\vec E_0}\cos (\omega t - kz)\)
En notation complexe, on notera le champ EM sous la forme :
\(\underline {\vec E} (z,t) = {\underline {\vec E} _0}\;{e^{i(\omega t - kz)}}\;\;\;\;\;et\;\;\;\;\;\underline {\vec B(} z,t) = {\underline {\vec B} _0}\;{e^{i(\omega t - kz)}}\)
Si la direction de l'onde est quelconque, dans la direction du vecteur unitaire \(\vec u\) :
\(\underline {\vec E} (x,y,z,t) = {\underline {\vec E} _0}\;{e^{i(\omega t - \vec k.\vec r)}}\;\;\;\;\;et\;\;\;\;\;\underline {\vec B(} x,y,z,t) = {\underline {\vec B} _0}\;{e^{i(\omega t - \vec k.\vec r)}}\)
où \(\vec k = k \vec u\) (\(\vec u\) vecteur unitaire donnant le sens de propagation) est le vecteur d'onde et \(\vec r = \vec {OM}\) (O, origine du repère et M le point d'observation).
