Questionnaire
Répondre à ce questionnaire juste après avoir visionné et étudié la vidéo "La physique animée".
Question
Quels ont été les domaines de recherches de Jean le Rond d'Alembert ?
Solution
Il n'a que 24 ans lorsqu'il entre à l'Académie des Sciences, et participera 10 ans plus tard avec Denis Diderot à la publication de « L'Encyclopédie ou Dictionnaire raisonné des sciences, des arts et des métiers ».
Ses travaux ont couvert de nombreux domaines tels que les mathématiques, la mécanique, l'hydrodynamique, l'optique, l'astronomie ainsi que la théorie de la musique et la philosophie.
Il s'est notamment intéressé, à la frontière entre les mathématiques et la physique, aux équations différentielles et aux dérivées partielles.
L'équation d'onde qui porte son nom est une équation aux dérivées partielles, établie en 1746 lors de l'étude des cordes vibrantes. Elle relie les variations temporelles du déplacement transversal d'une corde vibrante à ses variations dans l'espace par l'intermédiaire de la vitesse de propagation de l'onde, encore appelée célérité de l'onde.
Question
Comment s'écrit la coordonnée verticale de la force de tension qui agit sur un élément de corde à l'abscisse x, en fonction de la tension \(T_0\) de la corde et du déplacement transverse \(y(x,t)\) ?
Solution
La force verticale est donnée par :
\(T_y=T_0\alpha (x,t)=T_0 \frac{\partial y(x,t)}{\partial x}\)
Question
Écrire l'équation de d'Alembert pour une corde.
Solution
L'équation de d'Alembert est :
\(\frac {\partial ^2 y(x,t)}{\partial ^2 x}-\frac{1}{c^2}\frac {\partial ^2 y(x,t)}{\partial ^2 t}=0\)
Avec :
\(c=\sqrt {\frac {T_0}{\mu}}\)
qui représente la vitesse de propagation des ondes dans la corde.
Question
Pourquoi dit-on qu'une onde se propage d'autant plus mal que le milieu est plus mou et plus inerte ?
Solution
La vitesse de propagation des ondes dans la corde est :
\(c=\sqrt {\frac {T_0}{\mu}}\)
On constate bien que \(c\) est d'autant plus petite que le milieu est "mou" (soit \(T_0\) "faible") et plus inerte (\(\mu\) "grande").
Question
La vitesse de propagation des ondes dépend-elle de la manière avec laquelle on met la corde en mouvement ?
Solution
Que la corde soit pincée, frottée ou tapée, on constate que la vitesse de propagation reste la même.
Elle augmente avec la « raideur » du milieu (donnée par la tension \(F\) de la corde) et diminue avec l'inertie (représentée ici par la masse volumique \(\mu\))
Question
Comment expliquer qualitativement qu'il existe seulement quelques fréquences autorisées lorsque le musicien joue de la guitare ?
Solution
Le guitariste met en vibration les cordes d'une guitare : il génère ainsi de nombreuses ondes progressives.
Seules certaines d'entre elles seront constructives après réflexions multiples.
On obtient finalement un système d'ondes stationnaires et on a des conditions aux limites de résonance de la corde.
L'onde obtenue se propage sur place : les nœuds et les ventres ne se déplacent pas le long de la corde.
Question
Définir les nœuds et les ventres de vibration.
Quelle distance sépare deux nœuds successifs et deux ventres successifs ?
Solution
On obtient finalement un système d'ondes stationnaires et on a des conditions aux limites de résonance de la corde.
L'amplitude de l'onde reste constamment nulle en certains points appelés nœuds de vibration et distants de \(\lambda /2\), où \(\lambda\) est la longueur d'onde de vibration.
Elle est maximale en un ventre de vibration.
Deux ventres de vibration successifs sont également distants de \(\lambda /2\).
Question
Comment retrouver très simplement la longueur d'onde puis la fréquence du mode n ?
Solution
Le chevalet et le sillet de la guitare, distants de L, sont situés à des nœuds de vibration.
Par conséquent, en notant n un entier naturel quelconque :
\(L=n\frac{\lambda_n}{2}\)
Où \(\lambda_n\) est la longueur d'onde associée au mode propre stationnaire de la corde, ainsi quantifié par l'entier n.
La fréquence est :
\(\nu_n=\frac{c}{\lambda_n}=n\frac{c}{2L}\)
Question
Donner la solution générale de l'équation de d'Alembert sous la forme d'ondes stationnaires.
Solution
L'équation de d'Alembert étant linéaire, la vibration globale de la corde \(y(x,t)\) pourra s'écrire comme la somme des contributions des différents modes :
\(y(x,t) = \sum\limits_{n = 1}^\infty {y_{0,n} \sin \left( {n\frac{\pi }{L}\;x - \psi _n } \right)\cos \left( {n\frac{{\pi c}}{L}t - \varphi _n } \right)}\)
Question
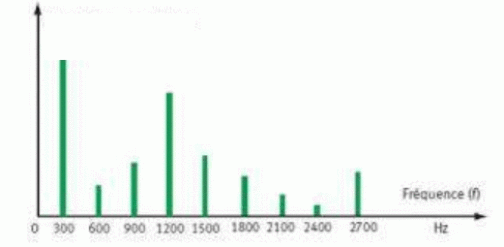
Définir le spectre acoustique d'un son.
Solution
On obtient le spectre acoustique du son en traçant l'amplitude du fondamental et de chaque harmonique en fonction de la fréquence.
Le nombre d'harmoniques dans un son complexe, ainsi que leurs amplitudes, dépendent de la nature de l'instrument de musique et lui confèrent sa propre caractéristique sonore que l'on appelle le timbre de l'instrument.
En résumé, l'amplitude de l'onde donne une intensité sonore forte ou faible, sa fréquence correspond à la hauteur du son : aigu ou grave, et le contenu spectral correspond à son timbre : chaud, sourd, strident, dur...
Par exemple, une guitare et un piano jouant la même note avec la même amplitude sonore produiront des sons dont le timbre est tout à fait différent.
Question
Estimer, en ordre de grandeur, la vitesse de propagation des ondes dans une corde de guitare.