Accélération d'un plateau sur deux cylindres
Consacrer 20 minutes de préparation à cet exercice.
Puis, si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Si vous avez des questions complémentaires, n'hésitez pas à les poser sur le forum.
Un système est constitué de deux rouleaux cylindriques (masse m et rayon R) sur lesquels est posé un plateau de masse M.
Les forces de frottement sont telles qu'il y a roulement sans glissement des rouleaux sur le plan incliné et par rapport au plateau.
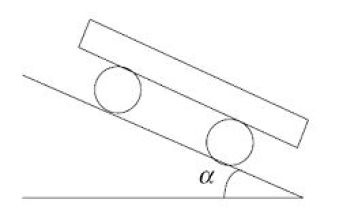
A l'instant initial, la vitesse des différents éléments du système est nulle dans le référentiel d'étude lié au plan incliné.
Question
Déterminer l'accélération du plateau.
On donne le moment d'inertie des rouleaux par rapport à un axe passant par leur centre de masse G :
\(J_G = \frac{1}{2}mR^2\)
Indice
Peut-on appliquer le théorème de la puissance cinétique à tout le système ?
Solution
On note v1 et v2 les vitesses (selon Ox) des centre d'inertie des deux roues, vP celle du plateau (animé d'un mouvement de translation pure) et ω la vitesse angulaire des roues.
Les conditions de roulement sans glissement s'écrivent :
Entre une roue et le plan incliné (I est le point de contact entre la roue et le plan incliné) :
\({\vec v_1} + \overrightarrow {IG} \wedge \vec \omega = \vec 0\;\;\;\;\;\;\;soit\;\;\;\;\;\;\;{v_1} + R\omega = 0\)
On remarque que les vitesses des roues sont identiques.
Entre une roue et le plateau (J est le point de contact entre la roue et le plateau) :
\({\vec v_1} + \overrightarrow {JG} \wedge \vec \omega = {\vec v_P}\;\;\;\;\;\;\;soit\;\;\;\;\;\;\;{v_1} - R\omega = {v_P}\)
On en déduit donc :
\({v_1} = {v_2} = v = - R\omega = \frac{{{v_P}}}{2}\)
Finalement, le système peut être décrit par une seule variable, par exemple la vitesse du plateau.
On va utiliser la conservation de l'énergie mécanique en présence de roulement sans glissement, ou plutôt le théorème de la puissance cinétique :
\(\frac{{d{E_c}}}{{dt}} = {P_{poids}}\)
Or :
\({E_c} = \frac{1}{2}Mv_P^2 + 2\left( {\frac{1}{2}m{v^2} + \frac{1}{2}J{\omega ^2}} \right)\)
Soit, après calculs :
\({E_c} = \left( {\frac{M}{2} + \frac{{3m}}{8}} \right)v_P^2\)
D'où :
\(\frac{{d{E_c}}}{{dt}} = \left( {M + \frac{{3m}}{4}} \right)v_P^{}{a_P}\)
La puissance des poids vaut :
\({P_{poids}} = M\vec g.{\vec v_P} + 2m\vec g.\vec v = (m + M)g\sin \alpha \;{v_P}\)
On en déduit l'accélération du plateau :
\({a_P} = \frac{{m + M}}{{\frac{3}{4}m + M}}g\sin \alpha\)
Simulation : Une animation JAVA de JJ.Rousseau (Université du Mans)
Plaque oscillante : cliquer