Chaîne sur le bord d'une table
Consacrer 20 minutes de préparation à cet exercice.
Puis, si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Si vous avez des questions complémentaires, n'hésitez pas à les poser sur le forum.
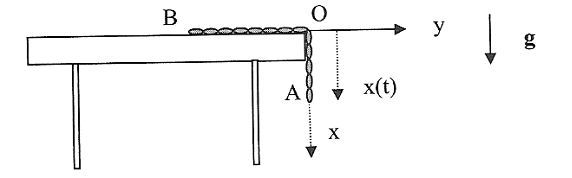
Une chaîne flexible AB de longueur L, de masse m répartie uniformément avec une masse linéique λ, se trouve initialement au repos sur le bord d'une table horizontale.
Une longueur a déborde de l'extrémité de la table.
La chaîne glisse sans frottement.
Le mouvement est décrit dans le repère galiléen (R) lié à la table.
On note x(t) l'abscisse instantanée de A.
Question
Exprimer l'énergie potentielle instantanée Ep de la chaîne. On prendra l'origine en x = 0.
Solution
La partie horizontale de la chaîne a une énergie potentielle nulle. La partie verticale de masse \(\lambda x\) dont le centre de masse a pour abscisse \(x/2\) a une énergie potentielle :
\(E_p=-\frac{1}{2}\lambda x^2 g\)
Question
En déduire x(t)
Indice
Comment justifier que l'énergie de la chaîne, corps déformable, se conserve bien ?
Solution
L'énergie mécanique de la chaîne se conserve :
\(\frac{d}{{dt}}\left( {\frac{1}{2}\lambda L{{\dot x}^2} - \frac{1}{2}\lambda {{\dot x}^2}g} \right) = 0\)
D'où l'équation différentielle vérifiée par x :
\(\ddot x - \frac{g}{L}x = 0\)
Dont la solution est de la forme :
\(x(t) = ach\left( {\sqrt {\frac{g}{L}} t} \right)\)
Question
Déterminer l'abscisse verticale du centre de masse G de la chaîne ainsi que son accélération verticale en fonction du temps.
Solution
Par définition, l'abscisse du centre d'inertie de la chaîne est :
\({x_G} = \frac{1}{{\lambda L}}\left( {\frac{{\lambda {x^2}}}{2}} \right) = \frac{{{x^2}}}{{2L}}\)
On calcule la vitesse :
\({v_{G,x}} = \frac{x}{L}\dot x = \frac{{{a^2}}}{2}\sqrt {\frac{g}{L}} \frac{1}{L}sh\left( {2\sqrt {\frac{g}{L}} t} \right)\)
Puis l'accélération :
\({a_{G,x}} = \frac{{{a^2}}}{{{L^2}}}gch\left( {2\sqrt {\frac{g}{L}} t} \right)\)
Question
Calculer la réaction de la table. La chaîne décolle-t-elle avant de quitter la table ?
Solution
Le théorème de la résultante cinétique appliqué à la chaîne et en en projection sur Ox donne :
\(m{a_{G,x}} = mg - N\)
D'où :
\(N = g\left( {1 - \frac{{{a^2}}}{{{L^2}}}ch\left( {2\sqrt {\frac{g}{L}} t} \right)} \right)\)
La chaîne décolle pour \(N=0\), soit à l'instant \(t_2\) :
\(ch\left( {2\sqrt {\frac{g}{L}} {t_2}} \right) = \frac{{{L^2}}}{{{a^2}}}\)
Elle quitte la table à l'instant \(t_1\) tel que :
\(ch\left( {\sqrt {\frac{g}{L}} {t_1}} \right) = \frac{L}{a}\)
On peut montrer que \(t_2<t_1\) : la chaîne décolle avant de quitter la table.