Étude d'un signal modulé en fréquence, applications
Une vidéo sur la modulation de fréquence (venant de l'armée américaine et datant de 1964)
Méthode : Principe de la vobulation du générateur BF
Regarder la notice du générateur BF utilisé pour l'utilisation de la vobulation :
Choisir une fréquence minimale \(f_{min}\) de l'odre de 2 kHz.
Choisir une fréquence maximale \(f_{max}\) de l'ordre de 20 kHz.
Visualiser la tension de rampe \(U_{wob}\) (prise à l'arrière du GBF).
Cette tension varie linéairement de la valeur nulle (correspondant à \(f_{min})\) jusqu'à la valeur de l'ordre de 10 V (correspondant à \(f_{max}\)).
Il existe une relation affine entre cette tension et la fréquence \(f\) de balayage :
\(f=aU_{wob}+b\)
Déterminer numériquement les coefficients \(a\) et \(b\).
On a ainsi réalisé un signal modulé en fréquence.
Exemple : Tracé automatique du diagramme de Bode d'un filtre passe-bande RLC
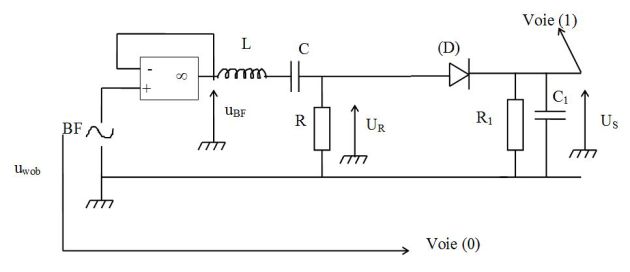
Réaliser le montage de la figure suivante.
On choisit :
\(L=12\; mH\) (\(500\) spires) ; \(C=100\;nF\) ; \(R=100\;\Omega\) ; \(C_1=1\;\mu m\) ; \(R_1=100\;k\Omega\)
Et (D) est une diode au germanium.
Aspect théorique :
Préciser le rôle du montage suiveur
Déterminer l'expression théorique du gain du montage.
Calculer la valeur théorique de la fréquence de résonance de tension aux bornes de la résistance R ainsi que la valeur de la bande passante du filtre passe-bande ainsi obtenu.
Préciser le rôle de la vobulation.
Quel est l'intérêt du montage "détecteur de crête" ?
Aspect expérimental :
Visualiser les tension \(u_R\) (avant le détecteur de crête) et \(U_{wob}\) en fonction du temps.
Expliquer l'allure de \(u_R\).
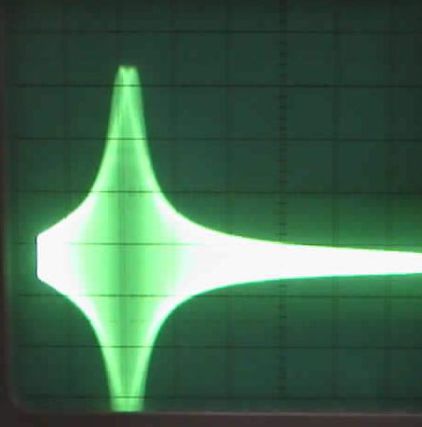
Visualiser à l'oscilloscope (en mode XY) la tension \(u_S\) en fonction de \(U_{wob}\).
Faire varier la vitesse de vobulation afin d'avoir une courbe stable.
Faire varier la valeur de R et observer l'évolution de la bande passante.