Oscillateur à pont de Wien
Exemple : Oscillateur à pont de Wien
Méthode : Filtre passe-bande
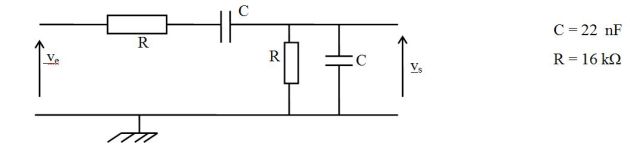
La fonction de transfert du circuit suivant (c'est un filtre passe-bande) est :
\({\underline H _1}(j\omega ) = \frac{Q}{{1 + jQ\left( {\frac{\omega }{{{\omega _0}}} - \frac{{{\omega _0}}}{\omega }} \right)}}\)
Avec :
\(\omega_0=1/RC\) et \(Q=1/3\).
Expérience :
Réaliser le montage avec les valeurs proposées sur la figure
Vérifier la nature du filtre obtenu
Évaluer expérimentalement \(Q\) et \(\omega_0\).
On rappelle que la largeur de la bande passante d'un filtre passe-bande est donnée par :
\(\Delta \omega = \frac {\omega_0}{Q}\)
Méthode : Réalisation de l'oscillateur
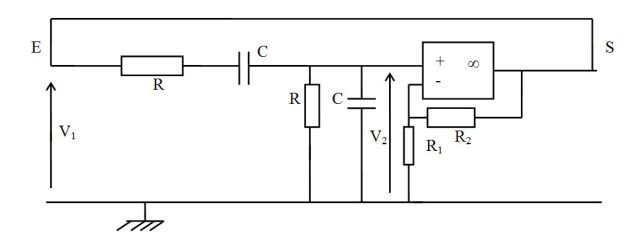
On réalise le montage de la figure suivante, avec :
\(R_2\) : une résistance de \(2,2\;k \Omega\)
\(R_1\) : une série de boîtes de \(1\; \Omega\), \(10\; \Omega\), \(100\; \Omega\) et \(1\;k \Omega\).
Les valeurs de \(R\) et de \(C\) sont celles données au paragraphe précédent.
Étude théorique :
Déterminer l'équation différentielle du second ordre vérifiée par \(v_2(t)\) (on posera \(K=1+R_2/R_1\)).
Calculer la valeur \(K\) nécessaire pour obtenir des oscillations sinusoïdales.
On choisit \(K>3\) avec \(R_2=2,2\;k \Omega\).
Justifier que la tension \(v_2(t)\) peut s'écrire :
\({v_2}(t) = A{e^{t/\tau }}\cos (\omega t + \varphi )\mathop {}\limits^{} \mathop {}\limits^{} si\mathop {}\limits^{} K < {K_1}\)
Donner la valeur de \(K_1\). Exprimer \(\tau\) et \(\omega\) en fonction de \(\omega_0\) et \(K\).
Calculer \(\tau\) et \(\omega\) pour \(K=4\).
Que donne le résultat mathématique concernant l'amplitude des oscillations si \(t>>\tau\) ?
Que se passe-t-il réellement ?
Comment évoluerait l'amplitude des oscillations pour \(K<3\) ?
Étude expérimentale :
Réaliser le montage :
Quel problème se pose pour l'obtention d'oscillations sinusoïdales pures ?
Mesurer la valeur de la pulsation du signal lorsque celui-ci est accroché.
La comparer avec celle qui assure le maximum du gain pour le pont de Wien.
Stabilisation en amplitude des oscillations sinusoïdales :
On reprend le montage précédent en supposant que des oscillations sinusoïdales de pulsation \(\omega\) et d'amplitudes \(V_2\) pour \(v_2(t)\) et \(V_1\) pour \(v_1(t)\) apparaissent.
On se propose de stabiliser les oscillations en prenant pour \(R_2\) une thermistance à coefficient de température négatif (CTN) suivant la loi :
\({R_2} = {R_{2_0}}{e^{ - \beta P}}\)
où \(P\) est la puissance électrique moyenne dissipée dans cet élément et \(\beta\) une constante positive.
Remplacer la résistance \(R_2\) par la CTN qui a ici une valeur de résistance de \(2,2\;k \Omega\) pour une température de 25°C.
Sa valeur augmente si la température décroît, et réciproquement.
Expliquer pourquoi ce dispositif permet de stabiliser les oscillations.
Faire varier \(R_1\) pour trouver les limites d'accrochage et de saturation du signal.